
5.方程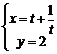 (t为参数)表示的曲线是( )。
(t为参数)表示的曲线是( )。
A 一条直线 B 两条射线 C 一条线段 D 抛物线的一部分
4.直线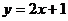 的参数方程是( )
的参数方程是( )
A 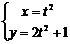 (t为参数) B
(t为参数) B 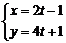 (t为参数)
(t为参数)
C 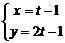 (t为参数)
D
(t为参数)
D 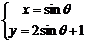 (t为参数)
(t为参数)
3.在同一坐标系中,将曲线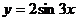 变为曲线
变为曲线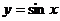 的伸缩变换是( )
的伸缩变换是( )
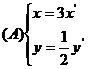
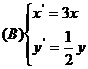
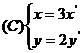
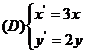
2.已知点 的极坐标是
的极坐标是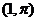 ,则过点
,则过点 且垂直极轴的直线方程是( )。
且垂直极轴的直线方程是( )。
A 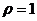 B
B 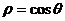 C
C 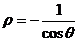 D
D 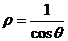
一、选择题
1.曲线的极坐标方程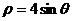 化为直角坐标为( )。
化为直角坐标为( )。
A 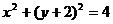 B
B 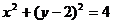 C
C 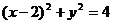 D
D 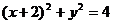
18.(14分)已知数列{an}的前n项和为Sn,且-1,Sn,an+1成等差数列,n∈N*,a1=1,函数f(x)=log3x.
(1)求数列{an }的通项公式;
}的通项公式;
(2)设数列{bn}满足bn=,记数列{bn}的前n项和为Tn,试比较Tn与-的大小.
解:(1)∵-1,Sn,an+1成等差数列.
∴2Sn=an+1-1,①
当n≥2时,2Sn-1=an-1,②
①-②,得2(Sn-Sn-1)=an+1-an,
∴3an=an+1.∴=3.(4分)
当n=1时,由①得2S1=2a1=a2-1,a1=1,
∴a2=3.∴=3.
∴{an}是以1为首项,3为公比的等比数列.
∴an=3n-1.(6分)
(2)∵f(x)= log3x,∴f(an)=log33n-1=n-1.
log3x,∴f(an)=log33n-1=n-1.
∴bn==
=.(8分)
∴Tn=
=
=-.(10分)
比较Tn与-的大小,只需比较2(n+2)(n+3)与312的大小即可.
2(n+2)(n+3)-312= 2(n2+5n+6-156)
2(n2+5n+6-156)
=2(n2+5n-150)
 =2(n+15)(n-10).
=2(n+15)(n-10).
∵n∈N*,
∴当1≤n≤9且n∈N*时,2(n+2)(n+3)<312 ,即Tn<-;
,即Tn<-;
当n=10时,2(n+2)(n+3)=312,即Tn= -;
-;
当n>10且n∈N*时,2(n+2)(n+3)>312,
即Tn>-.(14分)
17.(12分)在△ABC中,内角A,B,C的对边分别为a,b,c,且满足(2a-c)cosB=bcosC.
(1)求内角B的大小;
(2)设m=(sinA,cos2A),n=(4k,1)(k>1),m·n的最大值为5,求k的值.
解:(1)由正弦定理及(2a-c)cosB=bcosC,
得(2sinA-sinC)cosB=si nBcosC,
nBcosC,
整理得:2sinAcosB=sinBcosC+sinCcosB=sin(B+C)=sinA,(4分)
∵A∈(0,π),
∴sinA≠0,故cosB=,∴B=.(6分)
(2)m·n=4ksinA+cos2A=-2sin2A+4ksinA+1,
其中A∈,设sinA=t,t∈(0,1],则m·n=-2t2+4kt+1=-2(t-k)2+1+2k2.
(8分)
又k>1,故当t=1时,m·n取得最大值.
由题意得-2+4k+1=5,解得k=.(12分)
16.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,cosB=,且·=-21.
(1)求△ABC的面积;
(2)若a=7,求角C.
解:( 1)∵·=||||cos(π-B)=-accosB=-ac=-21,∴ac=35.(2分)
1)∵·=||||cos(π-B)=-accosB=-ac=-21,∴ac=35.(2分)
又∵cosB=,且B∈(0,π),
∴sinB==.
∴S△ABC=ac·sinB=×35×=14.
(6分)
(2)由(1)知ac=35,又a=7,∴c=5.
∴b2=49+25-2×7×5×=32.∴b=4.(8分)
由正弦定理得=.即=,
∴sinC=,
又∵a>c,∴C∈,∴C=.(12分)
三、解答题:本大题共4小题,满分50分.
15.(12分)解关于x的不等式x2-2ax+2≤0(a∈R).
解:因为Δ=4a2-8,所以当Δ<0即-<a<时,原不等式的解集为∅;(2分)
当Δ=0即a=±,对应的方程有两个相等实根.
(4分)
当a=时,原不等式的解集是{x|x=};
(6分)
当a=-时,原不等式的解集是{x|x=-};
(8分)
当Δ>0时,对应的方程有两个不等实根,分别为x1=a-,x2=a+,且x1<x2,所以不等式的解集是{x|a-≤x≤a+}.(12分)
14.已知实数x,y满足2x+y≥1,则u=x2+y2+4x-2y的最小值为 __________.
__________.
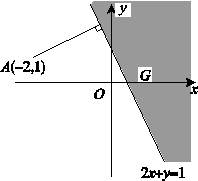
解析:由u=x2+y2+4x-2y=(x+2)2+(y-1)2-5知,u表示点P(x,y)与定点A(-2,1)的距离的平方与5的差.
又由约束条件2x+y≥1知:
点P(x,y)在直线l:2x+y=1上及其右上方.
问题转化为求定点A(-2,1)到由2x+y≥1所确定的平面区域的最近距离 .故A到直线l的距离为A到区域G上点的距离的最小值.
.故A到直线l的距离为A到区域G上点的距离的最小值.
d==,
∴d2=,∴umin=d2-5=-.
答案:-
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com