
6.如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于G.给出四个结论:①AE=CF;②EF=AP;③△EPF是等腰直角三角形;④∠AEP=∠AGF.其中正确的结论有( )
|
|
A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
5.如图,BC∥AM,∠A=90°,∠BCD=75°,点E在AB上,△CDE为等边三角形,BM交 CD于F,下列结论:①∠ADE=45°,②AB=BC,③EF⊥CD,④若∠AMB=30°,则CF=DF.其中正确的有( )
|
|
A. |
①②③ |
B. |
①②④ |
C. |
①③④ |
D. |
②③④ |
4.如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;④ =1.其中正确的是( )
|
|
A. |
①②③ |
B. |
①②④ |
C. |
①③④ |
D. |
①②③④ |
3.如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:
①AG=CE ②DG=DE
③BG﹣AC=CE ④S△BDG﹣S△CDE= S△ABC
其中总是成立的是( )
|
|
A. |
①②③ |
B. |
①②③④ |
C. |
②③④ |
D.
|
①②④ |
2.如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,点P是腰AD上的一个动点,要使PC+PB最小,则点P应该满足( )
|
|
A. |
PB=PC |
B. |
PA=PD |
C. |
∠BPC=90° |
D. |
∠APB=∠DPC |
一.选择题
1.已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP.其中正确的有( )个.
|
|
A. |
①②③ |
B. |
①②④ |
C. |
①③④ |
D. |
①②③④ |
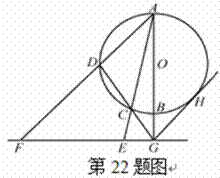
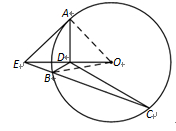
20.(2014吉林省长春市高中毕业班第二次调研 测试,22) 选修4—1:几何证明选讲.
测试,22) 选修4—1:几何证明选讲.
如图,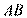 是圆
是圆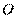 的直径,
的直径,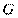 是
是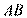 延长线上的一点,
延长线上的一点,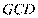 是圆
是圆
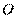 的割线,过点
的割线,过点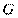 作
作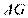 的垂线,交直线
的垂线,交直线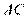 于点
于点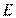 ,交直线
,交直线
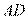 于点
于点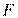 ,过点
,过点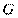 作圆
作圆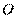 的切线,切点为
的切线,切点为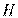 .
.
(1)求证: 四点共圆;(2)若
四点共圆;(2)若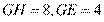 , 求
, 求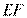 的长.
的长.
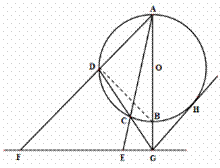
[解析] 20. (1)证明:连结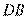 ,∵
,∵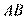 是圆
是圆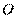 的直径,
的直径,
∴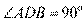 ,
,
在 和
和 中,
中,
又∵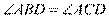 ∴
∴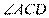
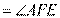
∴ 四点共圆。
四点共圆。
(2) ∵
∵ 四点共圆,∴
四点共圆,∴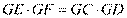
∵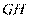 是圆
是圆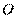 的切线,∴
的切线,∴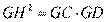 ∴
∴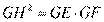
又因为 ∴
∴
∴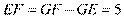 .
.
答案和解析
理数
[答案] 1. 
[解析] 1. 在Rt△ABC中,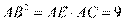 , 解得
, 解得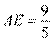 ; 同理可得
; 同理可得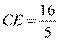 , 由射影定理可得
, 由射影定理可得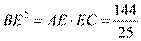 ,得
,得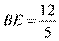 . 根据割线定理可得
. 根据割线定理可得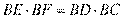 , 得
, 得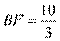 , 所以
, 所以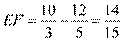 .
.
[答案] 2. 15
[解析] 2. 根据相交弦定理可得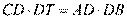 ,结合条件可得DT=9. 根据切割线定理可得
,结合条件可得DT=9. 根据切割线定理可得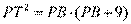 ①. 在Rt△DTP中,
①. 在Rt△DTP中,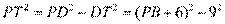 ②. ①②联立得PB=15.
②. ①②联立得PB=15.
[答案] 3. 
[解析] 3. 根据切割线定理可得 , 得
, 得 . 连接OC, 在Rt△OCP中, 根据射影定理可得PC2=
. 连接OC, 在Rt△OCP中, 根据射影定理可得PC2=  , 得PD=3, 又因为
, 得PD=3, 又因为 CD2=
CD2=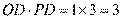 , 所以CD的长为
, 所以CD的长为 .
.
[答案] 4.6
[解析] 4.由割线定理得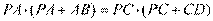 ,
,
所以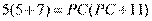 ,解得
,解得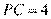 或
或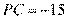 (舍去),
(舍去),
由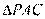 ~
~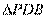 ,所以
,所以 ,所以
,所以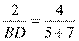 ,解得
,解得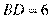 .
.
[答案] 5. 
[解析] 5. 因为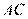 为圆的切线,由弦切角定理,则
为圆的切线,由弦切角定理,则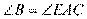 ,
,
又因为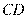 平分
平分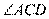 ,则
,则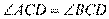 ,
,
所以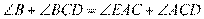 ,
,
根据三角形外角定理,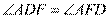 ,
,
因为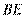 是圆
是圆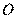 的直径,则
的直径,则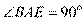 ,所以
,所以 是等腰直角三角形,
是等腰直角三角形,
所以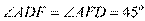 .
.
[答案] 6.①②
[解析] 6. 如图,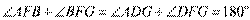 ,
, 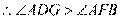 ,所以③错,所以正确的序号为①②.
,所以③错,所以正确的序号为①②.
范围 .
.
[答案] 7.1
[解析] 7. 由已知可得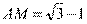 ,
,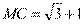 ,
,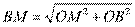
 ,由相交弦定理得:
,由相交弦定理得: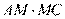
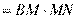 ,所以
,所以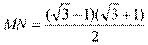
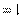
[答案] 8.7
[解析] 8.由题意可得: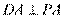 , 又因为
, 又因为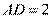 ,
, ,所以
,所以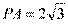 ,
,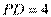 . 从而
. 从而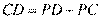
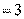 。由切割线定理
。由切割线定理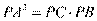 可得
可得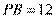 ,所以
,所以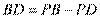
 . 再由相交弦定理
. 再由相交弦定理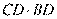
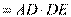 ,所以
,所以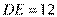 . 故直径
. 故直径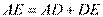
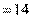 ,从而半径为7.
,从而半径为7.
[答案] 9.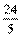
[解析] 9. 依题意,由切割线定理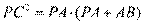 ,所以
,所以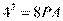 ,即
,即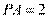 ,所以圆的半径
,所以圆的半径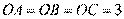 ,由
,由 为切线,所以
为切线,所以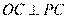 ,所以
,所以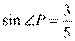 ,又弦
,又弦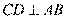 于点
于点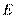 ,所以
,所以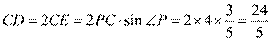 .
.
[答案] 10. 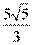
[解析] 10. 根据切割线定理可得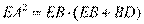 ,代入数据得EB=5. 因为AB=AC,可得∠C=∠ABC,又因为EA是切线,根据同弧对应的圆周角相等可得,∠C=∠EAB,所以可得∠EAB=∠ABC,所以可得EA//BC,又因为BE//AC,所以四边形ACBE为平行四边形,所以AC=EB=5,BC=EA=
,代入数据得EB=5. 因为AB=AC,可得∠C=∠ABC,又因为EA是切线,根据同弧对应的圆周角相等可得,∠C=∠EAB,所以可得∠EAB=∠ABC,所以可得EA//BC,又因为BE//AC,所以四边形ACBE为平行四边形,所以AC=EB=5,BC=EA=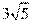 . 因为AC//BD,所以可得弧AB
. 因为AC//BD,所以可得弧AB 与弧CD相等,所以可得∠FACA=∠ACB,所以△AFC∽△BAC,可得
与弧CD相等,所以可得∠FACA=∠ACB,所以△AFC∽△BAC,可得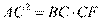 ,代入数据得
,代入数据得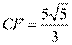 .
.
[答案] 11. 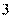
[解析] 11. 延长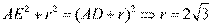 ,又
,又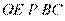 ,所以
,所以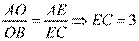 .
.
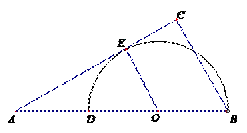
[答案] 12.查看解析
[解析] 12.(1)延长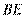 交圆
交圆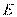 于点
于点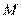 ,连结
,连结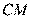 ,
,
则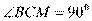 ,
,
又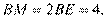
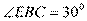 ,所以
,所以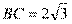 ,
,
又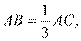 可知
可知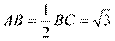 ,所以
,所以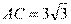
根据切割线定理得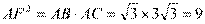 ,即
,即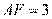 .
.
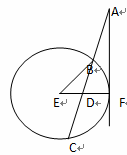
⑾证明:过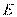 作
作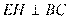 于
于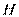 ,则
,则 ,
,
从而有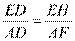 ,又由题意知
,又由题意知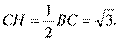

所以 ,因此
,因此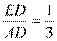 ,即
,即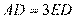
[答案] 13.查看解析
[解析] 13.


[答案] 14.查看解析
[解析] 14.(Ⅰ)因为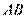 为圆
为圆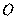 一条直径,所以
一条直径,所以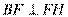 ,又
,又 ,
,
故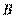 、
、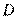 、
、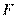 、
、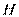 四点在以
四点在以 为直径的圆上,
为直径的圆上,
所以,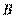 、
、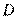 、
、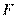 、
、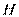 四点共圆. (4分)
四点共圆. (4分)
(Ⅱ)因为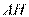 与圆
与圆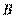 相切于点
相切于点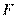 ,由切割线定理得
,由切割线定理得
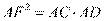 , 即
, 即 ,
,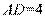 ,
,
所以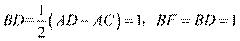
又 ,
,
则 , 得
, 得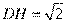 ,
,
连接 , 由(1)可知
, 由(1)可知 为
为 的外接圆直径,
的外接圆直径,
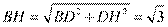 , 故
, 故 的外接圆半径为
的外接圆半径为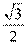 . (10分)
. (10分)
[答案] 15.查看解析
[解析] 15.(Ⅰ)连结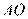 ,则
,则 . 由射影定理得
. 由射影定理得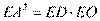 ,
,
由切割线定理得 ,故
,故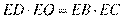 ,即
,即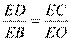 ,
,
又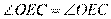 ,所以
,所以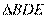 ~
~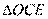 ,所以
,所以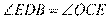 .
.
因此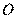 ,
, ,
,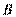 ,
,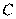 四点共圆. (6分)
四点共圆. (6分)
(Ⅱ)连结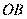 . 因为
. 因为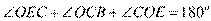 ,结合(Ⅰ)得
,结合(Ⅰ)得
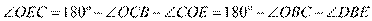
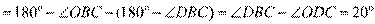 . (10分)
. (10分)
[答案] 16.查看解析
[解析] 16.(Ⅰ)连结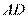 ,因为
,因为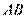 为圆的直径,
为圆的直径,
所以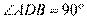 ,又
,又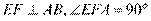 ,
,
则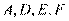 四点共圆,
四点共圆,
所以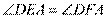 . (5分)
. (5分)
(Ⅱ)由(Ⅰ)知,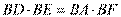 ,连结
,连结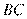 ,
,
又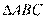 ∽
∽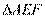 ,所以
,所以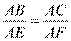
即 ,
,
所以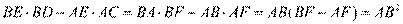 . (10分)
. (10分)
[答案] 17.查看解析
[解析] 17.(Ⅰ)连结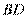 ,则
,则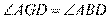 ,
,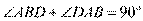 ,
,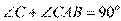 ,
,
所以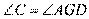 ,所以
,所以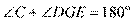 ,
,
所以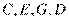 四点共圆. (5分)
四点共圆. (5分)
(Ⅱ)因为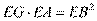 ,则
,则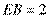 ,
,
又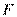 为
为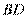 的三等分点,
的三等分点,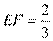 ,
,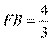 ,
,
又因为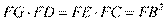 ,所以
,所以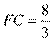 ,
,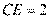 . (10分)
. (10分)
[答案] 18.查看解析
[解析] 18.22.(I)证明:连结OD,可得∠ODA=∠OAD=∠DAC …………………2分
∴OD//AE 又AE⊥DE …………………………………3分
∴OE⊥OD,又OD为半径
∴DE是的⊙O切线 ………………………5分
(II)解:过D作DH⊥AB于H,
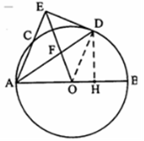
则有∠DOH=∠CAB
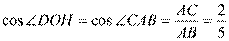 …………6分
…………6分
设OD=5x,则AB=10x,OH=2x,
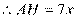
由△AED≌△AHD可得AE=AH=7x ……………8分
又由△AEF∽△DOF 可得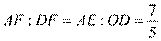
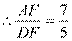 ……………………………………………………10分
……………………………………………………10分
[答案] 19.查看解析
[解析] 19 .
.
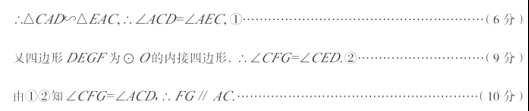
[答案] 20.查看解析
[解析] 20. (1)证明:连结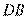 ,∵
,∵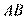 是圆
是圆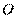 的直径,
的直径,
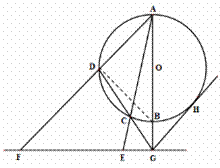
∴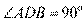 ,
,
在 和
和 中,
中,
又∵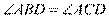 ∴
∴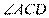
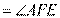
∴ 四点共圆。
四点共圆。
(2)∵ 四点共圆,∴
四点共圆,∴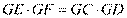
∵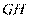 是圆
是圆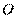 的切线,∴
的切线,∴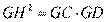 ∴
∴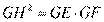
又因为 ∴
∴
∴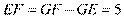 .
.
19.(2014河南豫东豫北十所名校高中毕业班阶段性测试(四)数学(理)试题, 22) 选修4-1: 几何证明选讲.
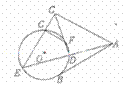
如图,AB是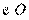 的一条切线,切点为B,ADE、CFD都是
的一条切线,切点为B,ADE、CFD都是 的割线, AC =AB,CE交
的割线, AC =AB,CE交 于点G.
于点G.
(I) 证明: ;
;
(Ⅱ) 证明:FG//AC.
[解析] 19.
18.(2014吉林实验中学高三年级第一次模拟,22)选修4—1几何证明选讲: 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F。
(I)求证:DE是⊙O的切线;
(II)若 的值.
的值.
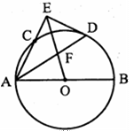
[解析] 18.22.(I)证明:连结OD,可得∠ODA=∠OAD=∠DAC …………………2分
∴OD//AE 又AE⊥DE …………………………………3分
∴OE⊥OD,又OD为半径
∴DE是的⊙O切线 ………………………5分
(II)解 :过D作DH⊥
:过D作DH⊥ AB于H,
AB于H,
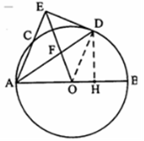
则有∠DOH=∠CAB
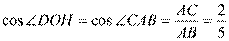 …………6分
…………6分
设OD=5x,则AB=10x,OH=2x,
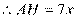
由△AED≌△AHD可得AE=AH=7x ……………8分
又由△AEF∽△DOF 可得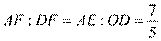
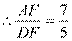 ……………………………………………………10分
……………………………………………………10分
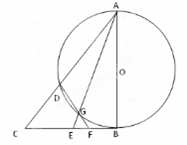
17. (2014黑龙江哈尔滨第三中学第一次高考模拟考试,22) 选修4-1:几何证明选讲
如图,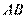 是的⊙
是的⊙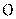 直径,
直径, 与⊙
与⊙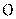 相切于
相切于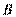 ,
,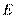 为线段
为线段 上一点,连接
上一点,连接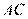 、
、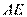
分别交⊙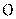 于
于 、
、 两点,连接
两点,连接 交
交 于点
于点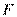 .
.
(Ⅰ)求证: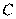 、
、 、
、 、
、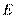 四点共圆.
四点共圆.
(Ⅱ)若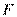 为
为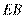 的三等分点且靠近
的三等分点且靠近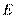 ,
,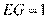 ,
,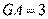 ,求线段
,求线段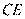 的长.
的长.
[解析] 17.(Ⅰ)连结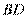 ,则
,则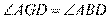 ,
,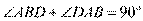 ,
,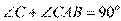 ,
,
所以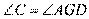 ,所以
,所以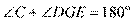 ,
,
所以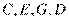 四点共圆. (5分)
四点共圆. (5分)
(Ⅱ)因为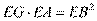 ,则
,则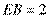 ,
,
又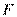 为
为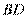 的三等分点,
的三等分点,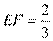 ,
,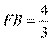 ,
,
又因为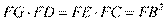 ,所以
,所以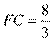 ,
,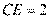 . (10分)
. (10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com