
18.(2014湖北武汉高三2月调研测试,22)
(Ⅰ)已知函数f(x) =ex-1-tx,∃x0∈R,使f(x0) ≤0,求实数t的取值范围;

[解析] 18.(Ⅰ)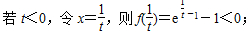
若t=0,f (x) =ex-1>0,不合题意;
若t>0,只需f(x) min≤0.
求导数,得f ′(x) =ex-1-t.
令f ′(x) =0,解得x=lnt+1.
当x<lnt+1时,f ′(x) <0,∴f(x) 在(-∞,lnt+1) 上是减函数;
当x>lnt+1时,f ′(x) >0,∴f(x) 在(lnt+1,+∞) 上是增函数.
故f(x) 在x=lnt+1处取得最小值f(lnt+1) =t-t(lnt+1) =-tlnt.
∴-tlnt≤0,由t>0,得lnt≥0,∴t≥1.
综上可知,实数t的取值范围为(-∞,0) ∪[1,+∞) .…………………………4分
(Ⅱ)由(Ⅰ),知f(x) ≥f(lnt+1) ,即ex-1-tx≥-tlnt.
取t=1,ex-1-x≥0,即x≤ex-1.
当x>0时,lnx≤x-1,当且仅当x=1时,等号成立,
故当x>0且x≠1时,有lnx<x-1.

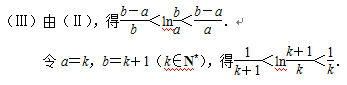
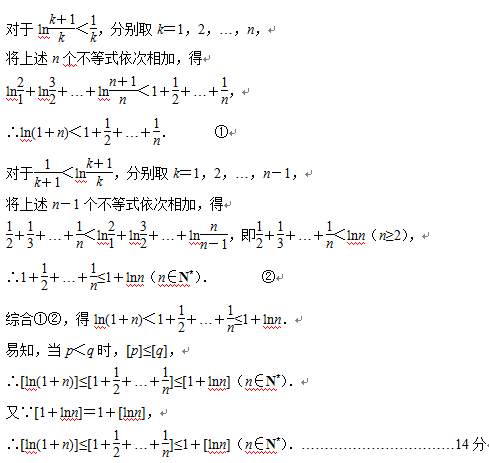
17.(2014江西重点中学协作体高三第一次联考数学(理)试题,21)已知函数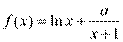 .
.
(1)当 时,证明对任意的
时,证明对任意的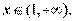
 ;
;
(2)求证: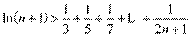
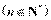 .
.
(3)若函数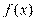 有且只有一个零点,求实数
有且只有一个零点,求实数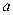 的取值范围.
的取值范围.
[解析] 17.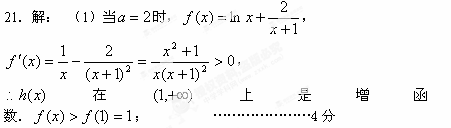 (2)根据(1)的结论,当
(2)根据(1)的结论,当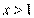 时,
时,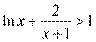 ,即
,即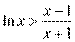 .
.
令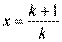 ,则有
,则有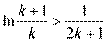 , ………………………7分
, ………………………7分
 .即
.即
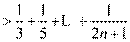 .…8分
.…8分
(本问也可用数学归纳法证明.)
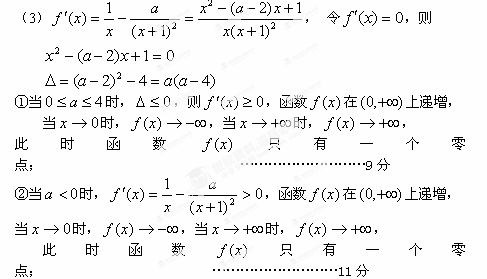 ③当
③当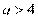 时,
时,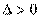 ,设
,设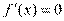 的两根分别为
的两根分别为 与
与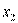 ,
,
则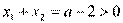 ,
,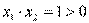 ,不妨设
,不妨设
当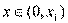 及
及 时,
时,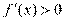 ,当
,当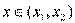 时,
时,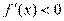 ,
,
所以函数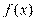 在
在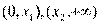 上递增,在
上递增,在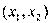 上递减,
上递减,
而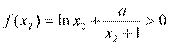
所以 时,
时,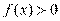 ,且
,且
因此函数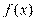 在
在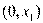 有一个零点,而在
有一个零点,而在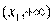 上无零点;
上无零点;
此时函数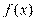 只有一个零点;
只有一个零点;
综上,函数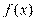 只有一个零点时,实数a的取值范围为R.………………………14分
只有一个零点时,实数a的取值范围为R.………………………14分
16. (2014北京东城高三第二学期教学检测,20) 在数列 ,
, 中,
中,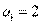 ,
,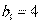 ,且
,且 成等差数列,
成等差数列, 成等比数列(
成等比数列(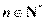 ).
).
(Ⅰ)求 ,
,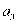 ,
,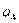 及
及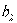 ,
,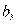 ,
, ,由此归纳出
,由此归纳出 ,
, 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)证明: .
.
[解析] 16.(Ⅰ)由条件得 ,
,
由此可得 .
.
猜测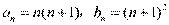 . (4分)
. (4分)
用数学归纳法证明:
①当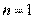 时,由上可得结论成立.
时,由上可得结论成立.
②假设当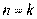 时,结论成立,即
时,结论成立,即 ,
,
那么当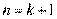 时,
时,
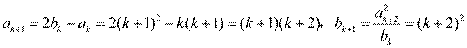 .
.
所以当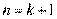 时,结论也成立.
时,结论也成立.
由①②,可知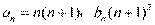 对一切正整数都成立. (7分)
对一切正整数都成立. (7分)
(Ⅱ)因为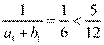 .
.
当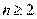 时,由(Ⅰ)知
时,由(Ⅰ)知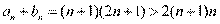 .
.
所以
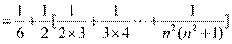
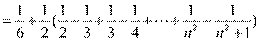
 .
.
综上所述,原不等式成立. (12分)
15.(2013安徽,14,5分)如图, 互不相同的点A1, A2, …, An, …和B1, B2, …, Bn, …分别在角O的两条边上, 所有AnBn相互平行, 且所有梯形AnBnBn+1An+1的面积均相等. 设OAn=an. 若a1=1, a2=2, 则数列{an}的通项公式是 .

[解析] 15.记△OA1B1的面积为S, 则△OA2B2的面积为4S.
从而四边形AnBnBn+1An+1的面积均为3S.
即得△OAnBn的面积为S+3(n-1) S=(3n-2) S.
∴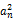 =3n-2, 即an=
=3n-2, 即an=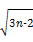 .
.
14.(2013安徽,15,5分)如图, 正方体ABCD-A1B1C1D1的棱长为1,
P为BC的中点, Q为线段 CC1上的动点, 过点A, P, Q的平面截该正方体所得的截面记为S.
则下列命题正确的是 (写出所有正确命题的编号).
CC1上的动点, 过点A, P, Q的平面截该正方体所得的截面记为S.
则下列命题正确的是 (写出所有正确命题的编号).
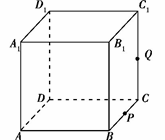
①当0< CQ<  时, S为四边形
时, S为四边形
②当CQ= 时, S为等腰梯形
时, S为等腰梯形
③当CQ= 时, S与C1D1的交点R满足C1R=
时, S与C1D1的交点R满足C1R=
④当 < CQ< 1时, S为六边形
< CQ< 1时, S为六边形
⑤当CQ=1时, S的面积为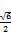
[解析] 14.过A作AM∥PQ交DD1或A1D1于M.
当0< CQ<  时, M在DD1上, 连MQ, 则截面为AMQP, 故①正确.
时, M在DD1上, 连MQ, 则截面为AMQP, 故①正确.
当CQ= 时, M与D1重合, 截面为AD1QP, 显然为等腰梯形,
②正确.
时, M与D1重合, 截面为AD1QP, 显然为等腰梯形,
②正确.
当CQ= 时, M在A1D1上, 且D1M=
时, M在A1D1上, 且D1M= .
.
过M作MR∥AP交C1D1于R, 则△MD1R∽△PBA, 从而D1R= , 即C1R=
, 即C1R= , 故③正确.
, 故③正确.
当 < CQ< 1时, 截面为AMRQP, 为五边形, 即④错误.
< CQ< 1时, 截面为AMRQP, 为五边形, 即④错误.
当CQ=1时, M为A1D1的中点, 截面AMC1P为菱形, 而AC1=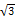 , PM=
, PM=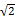 , 故面积为
, 故面积为 ×
×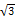 ×
×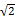 =
=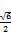 , ⑤正确.
, ⑤正确.
13.(2013陕西,14,5分)观察下列等式
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
……
照此规律, 第n个等式可为 .
[解析] 13.左边为平方项的(-1) n-1倍的和, 右边为(1+2+3+…+n) 的(-1) n-1倍. 再用数学归纳法证明成立.
12.(2013湖北,14,5分)古希腊毕达哥拉斯学派的数学家研究过各种多边形数. 如三角形数1,3, 6,10, …, 第n个三角形数为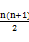 =
= n2+
n2+ n. 记第n个k边形数为N(n, k) (k≥3), 以下列出了部分k边形数中第n个数的表达式:
n. 记第n个k边形数为N(n, k) (k≥3), 以下列出了部分k边形数中第n个数的表达式:
三角形数 N(n, 3) = n2+
n2+ n,
n,
正方形数 N(n, 4) =n2,
五边形数 N(n, 5) = n2-
n2- n,
n,
六边形数 N(n, 6) =2n2-n,
……
可以推测N(n, k) 的表达式, 由此计算N(10,24) = .
[解析] 12.由N(n, 3) = n2+
n2+ n,
n,
N(n, 4) = n2+
n2+ n,
n,
N(n, 5) =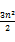 +
+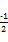 n,
n,
N (n, 6) =
(n, 6) = n2+
n2+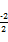 n,
n,
推测N(n, k) =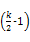 n2-
n2-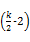 n, k≥3.
n, k≥3.
从而N(n, 24) =11n2-10n, N(10,24) =1 000.
11.(2013四川,15,5分)设P1, P2, …, Pn为平面α内的n个点. 在平面α内的所有点中, 若点P到点P1, P2, …, Pn的距离之和最小, 则称点P为点P1, P2, …, Pn的一个“中位点”. 例如, 线段AB上的任意点都是端点A, B的中位点. 现有下列命题:
①若三个点A, B, C共线, C在线段AB上, 则C是A, B, C的中位点;
②直角三角形斜边的中点是该直角三角形三个顶点的中位点;
③若四个点A, B, C, D共线, 则它们的中位点存在且唯一;
④梯形对角线的交点是该梯形四个顶点的唯一中位点.
其中的真命题是 . (写出所有真命题的序号)
[解析] 11.对①, 不妨设P为平面内任一点, ∴|PA|+|PB|≥|AB|=|AC|+|CB|. 故C是A, B, C的中位 点. 对②, 设C是Rt△ABC的直角顶点, 斜边AB的中点为D. 于是|DA|+|DB|+|DC|=3|DC|.
但|CA|+|CB|≤
点. 对②, 设C是Rt△ABC的直角顶点, 斜边AB的中点为D. 于是|DA|+|DB|+|DC|=3|DC|.
但|CA|+|CB|≤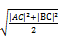 ·2=2
·2=2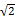 |DC|< 3|DC|, 故D不是A, B, C的中位点. 对③, 不妨设A、B、C、D是顺次的四个点,
P是平面内任一点, 点O为P在直线AB上的射影,
∴|PA|+|PB|+|PC|+|PD|≥|OA|+|OB|+|OC|+|OD|≥2|BC|+|CD|+|AB|. 由P的任意性知, 只要O点落在线段BC上即可,
③错. 对④, 设梯形ABCD的对角线AC, BD相交于O点, 由于|PA|+|PC|≥|AC|, |PB|+|PD|≥|BD|.
|DC|< 3|DC|, 故D不是A, B, C的中位点. 对③, 不妨设A、B、C、D是顺次的四个点,
P是平面内任一点, 点O为P在直线AB上的射影,
∴|PA|+|PB|+|PC|+|PD|≥|OA|+|OB|+|OC|+|OD|≥2|BC|+|CD|+|AB|. 由P的任意性知, 只要O点落在线段BC上即可,
③错. 对④, 设梯形ABCD的对角线AC, BD相交于O点, 由于|PA|+|PC|≥|AC|, |PB|+|PD|≥|BD|.
∴|PA|+|PC|+|PB|+|PD|≥|AC|+|BD|=|AO|+|OB|+|OC|+|OD|, 即O为该梯形四个顶点的唯一的中位点.
10.(2014湖北武汉高三2月调研测试,13) 如下图①②③④所示,它们都是由小正方形组成的图案.现按同样的排列规则进行排列,记第n个图形包含的小正方形个数为f(n) ,则
(Ⅰ)f(5) = ;
(Ⅱ)f(n) = .

[解析] 10. (1)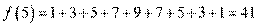
(2)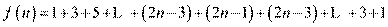
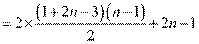 =
=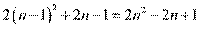
9.(2014江西红色六校高三第二次联考理数试题,11)观察下列不等式:①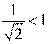 ;②
;②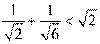 ;③
;③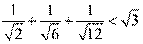 ;…则第
;…则第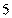 个不等式为 .
个不等式为 .
[解析] 9. 观察可得不等式左边的分母被开方数满足6-2、12-6成等差数列,不等式右边1,2, 3也成等差数列,所以第5个不等式为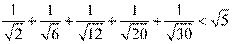 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com