22．(本小题满分12分)当m为何值时，直线(2m²＋m－3)x＋(m²－m)y＝4m－1.

(1)倾斜角为45°；

(2)在x轴上的截距为1.

详解答案

1[答案]　A

[解析]　斜率k＝＝，∴倾斜角为30°.

[解析]　由条件知k_BC＝k_AC，

∴＝，∴b＝－9.

2[答案]　D

3[答案]　C

[解析]　由直线方程的点斜式得y－2＝tan30°(x－1)，

整理得x－3y＋6－＝0.

4[答案]　A

[解析]　∵A₁B₂－A₂B₁＝3×3－1×(－2)＝11≠0，

∴这两条直线相交．

5[答案]　A

[解析]　直线变形为m(x＋2)－(y－1)＝0，故无论m取何值，点(－2,1)都在此直线上，∴选A.

6[答案]　A

[解析]　∵ab<0，bc<0，∴a，b，c均不为零，在直线方程ax＋by＋c＝0中，令x＝0得，y＝－>0，令y＝0得x＝－，∵ab<0，bc<0，∴ab²c>0，∴ac>0，∴－<0，∴直线通过第一、二、三象限，故选A.

7[答案]　B

[解析]　直线方程y＝－x化为一般式x＋y＝0，

则d＝.

8[答案]　C

[解析]　直线y＝－2x＋3的斜率为－2，则所求直线斜率k＝－2，直线方程y＝3x＋4中，令y＝0，则x＝－，即所求直线与x轴交点坐标为(－，0)．故所求直线方程为y＝－2(x＋)，即y＝－2x－.

9[答案]　D

[解析]　∵两直线互相垂直，∴a·(a＋2)＝－1，

∴a²＋2a＋1＝0，∴a＝－1.

10[答案]　B

[解析]　∵两条直角边互相垂直，

∴其斜率k₁，k₂应满足k₁k₂＝－1，排除A、C、D，故选B.

11[答案]　A

[解析]　k_PA＝－4，k_PB＝，画图观察可知k≥或k≤－4.

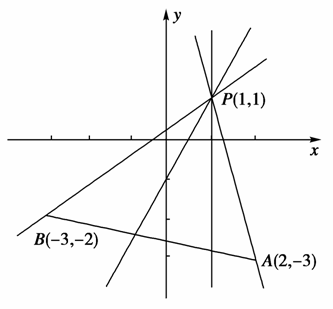
12[答案]　B

[解析]　由平面几何知，与A距离为1的点的轨迹是以A为圆心，以1为半径的⊙A，与B距离为2的点的轨迹是半径为2的⊙B，显然⊙A和⊙B相交，符合条件的直线为它们的公切线有2条．

13[答案]　5

[解析]　|AB|＝＝5.

14[答案]　

[解析]　直线l₂的方程可化为x－y＋＝0，

则d＝＝.

15[答案]　x＋y－5＝0　x－y＋1＝0

[解析]　设直线l的方程为＋＝1，则解得a＝5，b＝5或a＝－1，b＝1，即直线l的方程为＋＝1或＋＝1，即x＋y－5＝0或x－y＋1＝0.

16[答案]　①⑤

[解析]　两平行线间的距离为

d＝＝，

由图知直线m与l₁的夹角为30°，l₁的倾斜角为45°，

所以直线m的倾斜角等于30°＋45°＝75°或45°－30°＝15°.

[点评]　本题考查直线的斜率、直线的倾斜角、两条平行线间的距离，考查数形结合的思想．是高考在直线知识命题中不多见的较为复杂的题目，但是只要基础扎实、方法灵活、思想深刻，这一问题还是不难解决的．所以在学习中知识是基础、方法是骨架、思想是灵魂，只有以思想方法统领知识才能在考试中以不变应万变．

17[解析]　过AB两点的直线方程是＝.

点斜式为：y＋1＝－(x－4)

斜截式为：y＝－x＋

截距式为：＋＝1.

18[解析]　(1)直线l₁的斜率k₁＝－1，直线l₂的斜率k₂＝a²－2，因为l₁∥l₂，所以a²－2＝－1且2a≠2，解得：a＝－1.所以当a＝－1时，直线l₁：y＝－x＋2a与直线l₂：y＝(a²－2)x＋2平行．

(2)直线l₁的斜率k₁＝2a－1，l₂的斜率k₂＝4，因为l₁⊥l₂，所以k₁k₂＝－1，即4(2a－1)＝－1，解得a＝.所以当a＝时，直线l₁：y

＝(2a－1)x＋3与直线l₂：y＝4x－3垂直．

19[解析]　(1)设C(x，y)，由AC的中点M在y轴上得，＝0，解得x＝－5.

由BC中点N在x轴上，得＝0，

∴y＝－3，∴C(－5，－3)

(2)由A、C两点坐标得M(0，－)．

由B、C两点坐标得N(1,0)．

∴直线MN的方程为x＋＝1.即5x－2y－5＝0.

20[解析]　设点A的坐标为(x₁，y₁)，因为点P是AB中点，则点B坐标为(6－x₁，－y₁)，因为点A、B分别在直线l₁和l₂上，有

解得

由两点式求得直线方程为8x－y－24＝0.

21[解析]　(1)直线AC的斜率k_AC＝＝－2

即：7x＋y＋3＝0(－1≤x≤0)．

∴直线BD的斜率k_BD＝，

∴直线BD的方程为y＝(x＋4)，即x－2y＋4＝0

(2)直线BC的斜率k_BC＝＝

∴EF的斜率k_EF＝－

线段BC的中点坐标为(－，2)

∴EF的方程为y－2＝－(x＋)

即6x＋8y－1＝0.

(3)AB的中点M(0，－3)，

∴直线CM的方程为：＝，

22[解析]　(1)倾斜角为45°，则斜率为1.

∴－＝1，解得m＝－1，m＝1(舍去)

直线方程为2x－2y－5＝0符合题意，∴m＝－1

(2)当y＝0时，x＝＝1，

解得m＝－，或m＝2

当m＝－，m＝2时都符合题意，

∴m＝－或2.

21．(本小题满分12分)已知△ABC的三个顶点A(4，－6)，B(－4,0)，C(－1,4)，求

(1)AC边上的高BD所在直线方程；

(2)BC边的垂直平分线EF所在直线方程；

(3)AB边的中线的方程．

20．(本小题满分12分)过点P(3,0)作一直线，使它夹在两直线l₁：2x－y－2＝0和l₂：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 x＋y＋3＝0之间的线段AB恰被P点平分，求此直线方程．

19．(本小题满分12分)在△ABC中，已知点A(5，－2)，B(7,3)，且边AC的中点M在y轴上，边BC的中点N在x轴上，求：

(1)顶点C的坐标；

(2)直线MN的方程．

18．(12分)(1)当a为何值时，直线l₁：y＝－x＋2a与直线l₂：y＝(a²－2)x＋2平行？

(2)当a为何值时，直线l₁：y＝(2a－1)x＋3与直线l₂：y＝4x－3垂直？

三、解答题

17．(本小题满分10分)求经过点A(－2,3)，B(4，－1)的直线的两点式方程，并把它化成点斜式，斜截式和截距式．

16．(2009·高考全国卷Ⅰ)若直线m被两平行线l₁：x－y＋1＝0与l₂：x－y＋3＝0所截得的线段的长为2，则m的倾斜角可以是①15°　②30°　③45°　④60°　⑤75°，其中正确答案的序号是________．(写出所有正确答案的序号)

15．若直线l经过点P(2,3)且与两坐标轴围成一个等腰直角三角形，则直线l的方程为________或________．

14．平行直线l₁：x－y＋1＝0与l₂：3x－3y＋1＝0的距离等于________．

二、填空题

13．已知点A(－1,2)，B(－4,6)，则|AB|等于________．