
3、如图所示,为了表达矩形MDNP的面积,设 DN=x,PN=y,则面积
S=xy, ①
①
 因为点P在AB上,由△APQ∽△ABF得
因为点P在AB上,由△APQ∽△ABF得
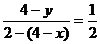 ,即
,即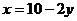 .
.
代入①,得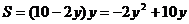 ,
,
即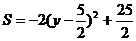 .
.
因为3≤y≤4,而y= 不在自变量的取值范围内,所以y=
不在自变量的取值范围内,所以y= 不是最值点,
不是最值点,
当y=3时,S=12;当 y=4时,S=8.故面积的最大值是S=12.
此时,钢板的最大利用率是80%。
二、1、2 2、 3、甲、乙 4、 5、6、 7、7 8、20
三1、有已知可得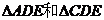 均为等腰直角三角形,计算得
均为等腰直角三角形,计算得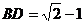 ,在直角三角形
,在直角三角形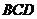 中,
中,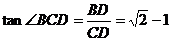 。
。
2、(1)设购买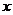 台甲机器,则
台甲机器,则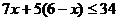 ,所以
,所以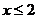 。即
。即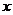 取0、1、2三个值,有三种购买方案:①不购买甲机器,购6台乙机器;②购买1台甲机器,5台乙机器;③购买2台甲机器,购4台乙机器。
取0、1、2三个值,有三种购买方案:①不购买甲机器,购6台乙机器;②购买1台甲机器,5台乙机器;③购买2台甲机器,购4台乙机器。
(2)按方案①,所需资金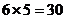 (万元),日产量为
(万元),日产量为 (个);按方案②,所需资金
(个);按方案②,所需资金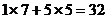 (万元),日产量为
(万元),日产量为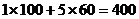 (个);按方案③,所需资金为
(个);按方案③,所需资金为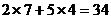 (万元),日产量为
(万元),日产量为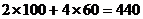 (个)。所以,选择方案②。
(个)。所以,选择方案②。
6、(14分)已知关于x的方程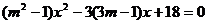 有两个正整数根(m 是整数)。
有两个正整数根(m 是整数)。
△ABC的三边a、b、c满足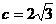 ,
,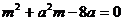 ,
,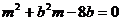 。
。
求:⑴ m的值;⑵ △ABC的面积。
师大附中2011年高一自主招生考试
数学试题参考答 案
案
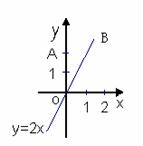
5、(12分)如右图,直线OB是一次函数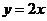 的图像,点A的坐标是(0,2),点C在直线OB
的图像,点A的坐标是(0,2),点C在直线OB
上且△ACO为等腰三角形,求C点坐标。
4、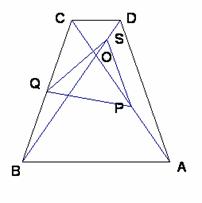 (12分)如图所示等腰梯形
(12分)如图所示等腰梯形 中,
中,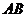 ∥
∥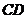 ,
,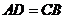 ,对角线
,对角线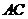 与
与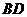 交于
交于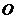 ,
,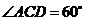 , 点
, 点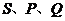 分别是
分别是 的中点。
的中点。
求证:△ 是等边三角形。
是等边三角形。
3、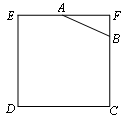 (12分)如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中
(12分)如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中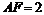 ,
,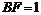 。为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率。
。为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率。
2、(12分)某公司为了扩大经营,决定购买6台机器用于生产活塞。现有甲、乙两种机器供选择,其中每种机器的价格和每台机器的日生产活塞数量如下表所示。经过预算,本次购买机器所需的资金不能超过34万元。
|
|
甲 |
乙 |
价格(万 元/台) 元/台) |
7 |
5 |
|
每台日产量(个) |
100 |
60 |
⑴ 按该公司的要求,可以有几种购买方案?
⑵ 若该公司购进的6台机器的日生产能力不能低于380个,为了节约资金,应选择哪种购买方案?
三、解答题
1、(10分)在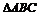 中,
中,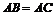 ,
,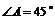 。
。 的垂直平分线分别交
的垂直平分线分别交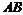 、
、 于
于 、
、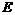 两点,连结
两点,连结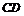 ,如果
,如果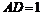 ,求:
,求: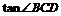 的值。
的值。
8、小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多
道。
7、已知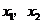 为方程
为方程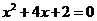 的两实根,
的两实根,
则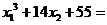 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com