3、在平面直角坐标系中，点P(-4，5)到x轴的距离为______，到y轴的距离为________.

一、填空题：

l、已知∠a的对顶角是81°，则∠a=______.

2、把“等角的补角相等”写成“如果…，那么…”的形式_________________________________.

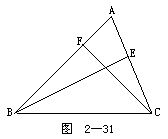
5．如图2-31所示．从锐角三角形ABC的顶点B，C分别向对边作垂线BE，CF．求证：

BC²=AB·BF+AC·CE．

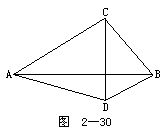
4．如图2-30所示．在四边形ADBC中，对角线AB⊥CD．求证：AC²+BD²=AD²+BC²．它的逆定理是否成立？证明你的结论．

3．由△ABC内任意一点O向三边BC，CA，AB分别作垂线，垂足分别是D，E，F．求证：

AF²+BD²+CE²=FB²+DC²+EA²．

2．已知矩形ABCD，P为矩形所在平面内的任意一点，求证：PA²+PC²=PB²+PD²．

　(提示：应分三种情形加以讨论，P在矩形内、P在矩形上、P在矩形外，均有这个结论．)

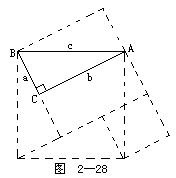
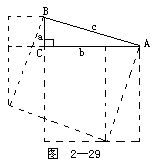
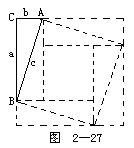
1．用下面各图验证勾股定理(虚线代表辅助线)：

　(1)赵君卿图(图2-27)；

　(2)项名达图(2-28)；

　(3)杨作枚图(图2-29)．

28.（8分）如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.

(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结 论.

(2)当点P移动到AB的外侧时,如图(2),是否仍有(1)的结论?如果不是，请写出你的猜想(不要求证明).

(3)当点P移动到如图(3)的位置时,∠P与∠A、∠C又有怎样的关系?能 否利用(1)的结论来证明?还有其他的方法吗?请写出一种.

27.（8分）某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备送给他们，如果每人送3本，则剩余8 本；如果前面每人送5本，则最后一人得到的课外读物不足3本，设该校买了 本课外读物，有 名学生获奖，请解答下列问题：

（1）用含 的代数式表示 ；

（2）求出该校的获奖人数及所买课外读物的本数.

26.（8分）已知方程组 的解 为非正数， 为负数.

（1）求 的取值范围；

（2）化简 ；

（3）在 的取值范围内， 是最大的整数， 是最小的整数，求 的值；

（4）在 的取值范围内，当 取何整数时，不等式 的解为 .