
5.
[答案] 6.(Ⅰ) 设矩阵M的 逆矩阵M-1=
逆矩阵M-1= , 则MM-1=
, 则MM-1= .
.
又M= , 所以
, 所以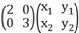 =
= ,
,
所以2x1=1, 2y1=0, 3x2=0, 3y2=1,
即x1= , y1=0, x2=0, y2=
, y1=0, x2=0, y2=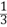 , 故所求的逆矩阵M-1=
, 故所求的逆矩阵M-1=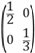 .
.
(Ⅱ) 设 曲线C上任意一点P(x, y) , 它在矩阵M所对应的线性变换作用下得到点P'(x',
y') , 则
曲线C上任意一点P(x, y) , 它在矩阵M所对应的线性变换作用下得到点P'(x',
y') , 则 =
=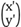 , 即
, 即
又点P'(x', y') 在曲线C'上,
所以 +y'2=1, 则
+y'2=1, 则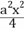 +b2y2=1为曲线C的方程.
+b2y2=1为曲线C的方程.
又已知曲线C的方程为x2+y2=1, 故
又a>0, b>0, 所以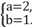
8.
答案和解析
理数
[答案] 1.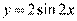 (或
(或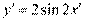 )
)
[解析] 1.MN=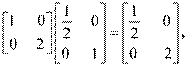 所以在矩阵MN变换下
所以在矩阵MN变换下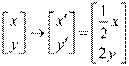 ,则
,则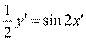 ,即
,即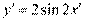 ,所以曲线
,所以曲线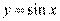 在矩阵MN变换下得到曲线C的
在矩阵MN变换下得到曲线C的 方程是
方程是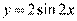 .
.
[答案] 2.查看解析
[解析] 2.(Ⅰ) 法一: 依题意, 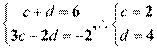 .
. 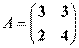 .
.
所以 . (4分)
. (4分)
法二: 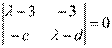 ,即
,即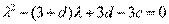 的两个根为6和1,
的两个根为6和1,
故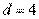 ,
, 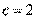 .
. 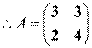 ,
, 所以
所以 ,
,
(Ⅱ) 法一: 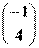 =2
=2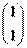 -
- ,A3
,A3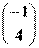 =2×63
=2×63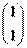 -13
-13 =
=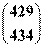 . (7分)
. (7分)
法二: 

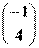 =
=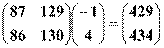 . (7分)
. (7分)
[答案] 3.查看解析
[解析] 3. 设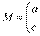
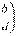 ,有已知得
,有已知得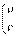
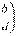

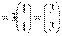 ,
,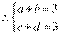 ,
,
又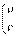
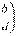
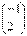
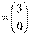 ,
,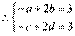 ,
,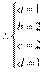 ,
,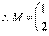
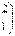 .
(7分)
.
(7分)
[答案] 4.查看解析
[解析] 4. 设曲线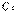
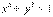 上任意一点
上任意一点 ,在矩阵
,在矩阵 所对应的变换作用下得到点
所对应的变换作用下得到点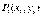 ,则
,则 ,即
,即 . (5分)
. (5分)
又点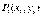 在曲线
在曲线 上,所以
上,所以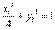 ,则
,则 为曲线
为曲线 的方程.
的方程.
又曲线 的方程为
的方程为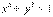 ,故
,故 ,
, ,
,
因为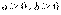 ,所以
,所以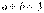 . (10分)
. (10分)
[ 答案] 5.A2=
答案] 5.A2= =
= .
.
设α=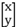 . 由A2α=β, 得
. 由A2α=β, 得 =
=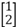 , 从而
, 从而
解得x=-1, y=2, 所以α=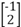 .
.
8.(2013江苏,21B, 10分)已知矩阵A= , B=
, B=
 , 求矩阵A-1B.
, 求矩阵A-1B.
7.
7.(20 13福建,21(1), 7分)已知直线l: ax+y=1在矩阵A=
13福建,21(1), 7分)已知直线l: ax+y=1在矩阵A=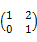 对应的变换作用下变为直线l': x+by=1.
对应的变换作用下变为直线l': x+by=1.
(Ⅰ) 求实数a, b的值;
(Ⅱ) 若点P(x0, y0) 在直线l上, 且A =
= , 求点P的坐标.
, 求点P的坐标.
6.
6.(2011福建, 21(1) , 7分) 选修4-2:矩阵与变换
设矩阵M=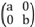 (其中a>0, b>0) .
(其中a>0, b>0) .
(Ⅰ) 若a=2, b=3, 求矩阵 M的逆矩阵M-1;
M的逆矩阵M-1;
(Ⅱ) 若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C': +y2=1, 求a, b的值.
+y2=1, 求a, b的值.
5.
5.(2011江苏, 21B, 10分) 选修4-2:矩阵与变换
已知矩阵A= , 向量β=
, 向量β=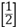 .
. 求向量α, 使得A2α=β.
求向量α, 使得A2α=β.
4. (2014江苏苏北四市高三期末统考, 21B) 设矩阵 (其中
(其中 ),若曲线
),若曲线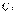
 在矩阵
在矩阵 所对应的变
所对应的变
换作用下得到曲线 ,求
,求 的值.
的值.
[解析] 4. 设曲线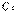
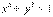 上任意一点
上任意一点 ,在矩阵
,在矩阵 所对应的变换作用下得到点
所对应的变换作用下得到点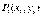
 ,则
,则 ,即
,即 . (5分)
. (5分)
又点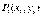 在曲线
在曲线 上,所以
上,所以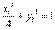 ,则
,则 为曲线
为曲线 的方程.
的方程.
又曲线 的方程为
的方程为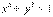 ,故
,故 ,
, ,
,
因为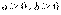 ,所以
,所以 . (10分)
. (10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com