一、选择题

1．绝对值小于101所有整数的和是（ 　）

（A）0　 （B）100　 （C）5050　 （D）200

26.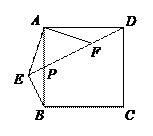 (本题10分)如图，正方形ABCD中，P是AB的中点，连接DP，过点B作BE⊥DP交DP的延长线于点E，连接AE，过点A作AF⊥AE交DP于点F，连接BF． （1）若AE=1，求EF的长； （2）求证：PF=EP+EB．

25．（本题9分）如图1，△ABC和△DBC都是边长为2的等边三角形。

（1）以图1中的某个点为旋转中心，旋转△DBC，就能使△DBC与△ABC重合，则满足题意的点为：　　　　　　　　　　　　　 （写出符合条件的所有点）；

（2）将△DBC沿BC方向平移得到△D₁B₁C₁，如图2、图3所示，则四边形ABD₁C₁是平行四边形吗？证明你的结论；

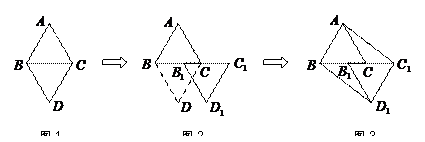（3）在(2)的条件下，当BB₁=_____时，四边形ABD₁C₁为矩形.

24.（本题8分）如图，四边形ABCD中，E、F、G、H分别是BC、AD、BD、AC的中点.

（1）求证：EF与GH互相平分；

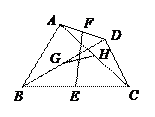　 　　　（2）当四边形ABCD的边满足条件　　 　　　　　时，EF⊥GH.

23．(本题7分)在一个不透明的口袋里装有若干个质地相同的红球, 为了估计袋中红球的数量，某学习小组做了摸球实验, 他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色, 再把它放回袋中, 多次重复摸球. 下表是多次活动汇总后统计的数据：

（1）请估计：当摸球次数S很大时, 摸到白球的频率将会接近　　　　　 ；

假如你去摸一次，你摸到红球的概率是　　　　　　 ；（精确到0.1）. （2）试估算口袋中红球有多少只?

22.（本题6分）为了保证中小学生每天锻炼1小时，某校开展了形式多样的体育活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图1和图2．

（1）请根据所给信息在图1中将表示“乒乓球”项目的图形补充完整；

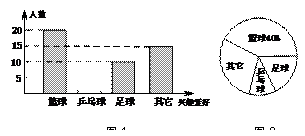（2）扇形统计图2中表示”足球”项目扇形的圆心角度数为　　　 　．

21.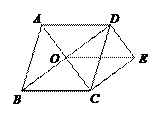 (本题8分)如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE．

求证：OE=BC．

20.（本题8分）如图，在□ABCD中，点E、F在BD上，BE=DF，求证：AE=CF．

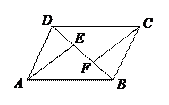
三、解答题 本大题共9小题，共74分．解答写出必要的解题过程、演算步骤或文字说明.

19．（本题8分）如图，方格纸中每个小正方形

的边长为1，△ABC的顶点均在格点上．

根据下列要求，利用直尺画图（不写作法）： （1）画出△ABC绕着点C按顺时针方向旋转

90°后的△A₁B₁C； （2）画出△ABC关于原点O对称的△A₂B₂C₂.