14.如图所示,空间有场强E=1.0×10² V/m竖直向下的电场,长L=0.8 m不可伸长的轻绳固定于O点.另一端系一质量m=0.5 kg带电q=5×1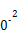　C的小球.拉起小球至绳水平后在A点无初速度释放,当小球运动至O点的正下方B点时,绳恰好断裂然后垂直打在同一竖直平面且与水平面成θ=53°、无限大的挡板MN上的C点,g取10 m/s².试求:

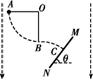
(1)绳子的最大张力T;

(2)A、C两点的电势差U_AC.

14:(1)30 N　(2)125 V

解析:(1)A→B由动能定理及圆周运动知识有:(mg+qE)·L=m,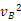

T-(mg+qE)=m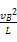　　解得T=30 N.

(2)A→C由功能关系及电场相关知识有:(mg+qE)h_AC=m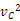

v_Csin θ=v_B,　　 U_AC=E·h_AC.

解得U_AC=125 V.

13．如图所示，一平行板电容器水平放置，板间距离为d，上极板开有一小孔，质量均为m、带电荷量均为＋q的两个带电小球(视为质点)，其间用长为l的绝缘轻杆相连，处于竖直状态，已知d＝2l，今使下端小球恰好位于小孔中，由静止释放，让两球竖直下落。当下端的小球到达下极板时，速度刚好为零。试求：

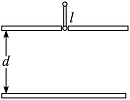
(1)两极板间匀强电场的电场强度；

(2)两球运动过程中的最大速度。

13：(1)　(2)

解析： (1)两球由静止开始下落到下端的小球到达下极板的过程中，由动能定理得2mgd－Eqd－Eq(d－l)＝0

解得E＝

(2)两球由静止开始下落至上端小球恰好进入小孔时两球达到最大速度，此过程利用动能定理得2mgl－Eql＝

解得v＝

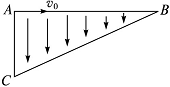
12．如图所示，在直角三角形区域ABC内存在着平行于AC方向的匀强电场，AC边长为l，一质量为m、电荷量为＋q的带电粒子以初速度v₀从A点沿AB方向进入电场，垂直通过BC边的中点，则粒子从BC出来时的水平分速度v_x和电场强度的大小E各为多大？(不计重力)

12：v₀　

解析：粒子水平方向做匀速直线运动，故从BC出来时的水平分速度v_x＝v₀，粒子在电场中做类平抛运动，在BC中点将末速度分解如图。

设速度的偏转角为θ，则

tan θ＝，v_y＝at＝×

在△ABC中，tan θ＝

故＝

所以E＝。

11.　18 　解析　以φ₂的电势为零，由能量守恒可知，电荷的电势能和动能的总和保持不变，由题意可知每经过一个等势面带电粒子的动能减少30 J，则在等势面φ₂上时动能为30 J，电势能为0，则总能量为30 J，故当电势能为12 J时，动能为18 J.

11.

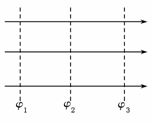
如图所示，实线为电场线，虚线为等势面，且相邻两等势面的电势差相等，一正电荷在等势面φ₃上时具有动能60 J，它运动到等势面φ₁上时，速度恰好为零，令φ₂＝0，那么，当该电荷的电势能为12 J时，其动能大小为________J.

10.　0　　 解析　由动能定理qU_AB＝ΔE_k＝0，所以U_AB＝0.

质点做匀速圆周运动R＝　　 静电力提供向心力有qE＝.

解得E＝.

二、非选择题

10．质量为m，电荷量为q的质点，在静电力作用下以恒定速率v沿圆弧由A运动到B，其速度方向改变θ角，AB弧长为s，则A、B两点的电势差U_AB＝________，AB中点的场强大小E＝________.

9．D　解析：设带电粒子初始速度方向为正方向，则其v-t图象如图所示。由图象可知带电粒子做往复运动，3 s末回到出发点，A、B错误；3 s末带电粒子速度为0,0～3 s内带电粒子的位移为0，电场力做的总功为0，D正确。

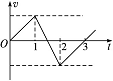
9．如图所示为匀强电场的电场强度E随时间t变化的图象。当t＝0时，在此匀强电场中由静止释放一个带正电的粒子，设带电粒子只受电场力的作用，则下列说法中正确的是(　　 )

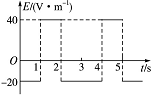
A．带电粒子将始终向同一个方向运动

B．2 s末带电粒子回到原出发点

C．3 s末带电粒子的速度不为零

D．0～3 s内，电场力做的总功为零

8.D解析:电子受到的电场力方向垂直于等势面且指向曲线的凹侧,所以电子受到的电场力

方向、电场强度的方向如图所示,可知a点的电势比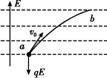

b点高,电子在a点的加速度方向垂直于等势面向下,选项A、B错误.电子从a点到b点电场力做负功,电子动能减少,电势能增加,选项C错误、D正确.