9. 一平行板电容器的两个极板水平放置，两极板间有一带电荷量不变的小油滴，油滴在极板间运动时所受空气阻力的大小与其速率成正比．若两极板间电压为零，经一段时间后，油滴以速率v匀速下降；若两极板间的电压为U，经一段时间后，油滴以速率v匀速上升．若两极板间电压为－U，油滴做匀速运动时速度的大小、方向将是(　)

A. 2v、向下　　　　　　　　　　　　　　　　 B. 2v、向上

C. 3v、向下　 　　　　　　　　　　　　　　　　　　　　　　　　 D. 3v、向上

解析：以油滴为研究对象，根据共点力平衡条件有：不加电压时，mg－kv＝0，所加电压为U时，mg＋kv－＝0，所加电压为－U时，mg＋－kv′＝0，联立以上各式得：v′＝3v，方向竖直向下．

答案：C

8. (多选)如图所示，M、N是竖直放置的两平行金属板，分别带等量异种电荷，两极板间产生一个水平向右的匀强电场，场强为E，一质量为m、电荷量为＋q的微粒，以初速度v₀竖直向上从两极正中间的A点射入匀强电场中，微粒垂直打到N极板上的C点，已知AB＝BC.不计空气阻力，则可知(　)

A. 微粒在电场中做抛物线运动

B. 微粒打到C点时的速率与射入电场时的速率相等

C. MN板间的电势差为2mv/q

D. MN板间的电势差为Ev/2g

解析：微粒所受合外力为恒力，故微粒做抛物线运动，A项正确；因AB＝BC，即·t＝·t可见v_C＝v₀，故B项正确；A→C由动能定理得：W_电－W_重＝ΔE_k＝0，所以W_电＝W_重，即：q＝mgh，而h＝，所以U＝，故C项错误；又由mg＝qE得q＝代入U＝，得U＝，故D项错误．

答案：AB

题组二　提能练

7. 如图所示，C为中间插有电介质的电容器，a和b为其两极板，a板接地．P和Q为两竖直放置的平行金属板，在两板间用绝缘线悬挂一带电小球．P板与b板用导线相连，Q板接地．开始时悬线静止在竖直方向，在b板带电后，悬线偏转了角度α.现在通过调节a、b间的距离，使悬线的偏角α变大，则在调节的过程中下列说法中正确的是(　)

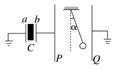
A．a、b间的距离在增大 　　　　　　　　　　　　　　　 B．电容器C的带电荷量在增大

C．a、b两极板间的电势差减小 　　　　　　　　　　 D．a、b两极板间的电场强度在增大

解析：在调节a、b间的距离时悬线的偏角α变大，说明P板上的带电荷量在增大，因而电容器C的带电荷量在减小，同时也表明电容器C的电容减小了，故a、b间的距离在增大，所以A正确、B错误；因为a板接地，在a、b间的距离增大的过程中，a板电势不变，所以a、b两板间的电势差增大，故C错误；因为a、b两板间的电场强度E＝，U＝，C＝，故a、b两板间的电场强度随电容器C的带电荷量的减小而减小，所以D错误．

答案：A

6. (多选)一个质量为m、电荷量为＋q的小球以初速度v₀水平抛出，在小球经过的竖直平面内，存在着若干个如图所示的无电场区和有理想上下边界的匀强电场区，两区域相互间隔、竖直高度相等，电场区水平方向无限长，已知每一电场区的场强大小相等、方向均竖直向上，不计空气阻力，下列说法正确的是(　)

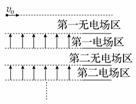
A. 小球在水平方向一直做匀速直线运动

B. 若场强大小等于，则小球经过每一电场区的时间均相同

C. 若场强大小等于，则小球经过每一无电场区的时间均相同

D. 无论场强大小如何，小球通过所有无电场区的时间均相同

解析：由于水平方向不受外力，A对；若mg＝qE，则小球在电场内竖直方向做匀速运动，由于经过无电场区一次就加速一次，则经电场区的时间越来越短，BD错；C选项中小球在竖直方向先加速后以同样大小加速度减速，周期性地向下运动，C对．

答案：AC

5. 如图所示竖直放置的两个平行金属板间存在匀强电场，与两板上边缘等高处有两个质量相同的带电小球，P小球从紧靠左极板处由静止释放，Q小球从两板正中央由静止释放，两小球最终都能运动到右极板上的同一位置，则从释放到运动到右极板的过程中它们的(　)

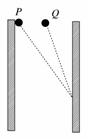
A. 运动时间t_P>t_Q

B. 电势能减少量之比ΔE_P∶ΔE_Q＝2∶1

C. 电荷量之比q_P∶q_Q＝2∶1

D. 动能增加量之比ΔE_kP∶ΔE_kQ＝4∶1

解析：两球均受重力、恒定的电场力作用，做匀加速直线运动，按运动的分解，竖直方向是重力作用下的自由落体运动，二者下降位移相同，运动时间相等，A错误；水平方向是电场力作用下的初速度为0的匀加速直线运动，位移之比x_P∶x_Q＝2∶1，由公式x＝t²得它们的电荷量之比q_P∶q_Q＝2∶1，C正确；又ΔE_P＝q_PU，ΔE_Q＝q_Q·，故ΔE_P∶ΔE_Q＝4∶1，B错误；动能增加量ΔE_kP＝ΔE_P＋mgh，ΔE_kQ＝ΔE_Q＋mgh，故ΔE_kP∶ΔE_kQ≠4∶1，D错误．

答案：C

4. (多选)如图，水平放置的三块带孔的平行金属板与一个直流电源相连，一个带正电的液滴从A板上方M点处由静止释放，不计空气阻力，设液滴电荷量不变．从释放到到达B板小孔处为过程Ⅰ，在BC之间运动为过程Ⅱ，则(　)

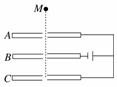
A．液滴一定能从C板小孔中穿出

B．过程Ⅰ中一定是重力势能向电势能和动能转化

C．过程Ⅰ和过程Ⅱ系统机械能变化量大小相等

D．过程Ⅱ中一定是重力势能向电势能和动能转化

解析：设MC之间的高度为H，A、B之间的电势差为U，则可得B、C之间的电势差为－U，M到C板小孔由动能定理可得：mgH＋qU－qU＝mv²，可得v＝，A正确；从A板小孔运动到B板小孔的过程中电势能减少，所以过程Ⅰ中重力势能和电势能向动能转化，B错误；由功能关系可得机械能的变化量取决于除重力以外的力所做的功，即电场力所做的功，在过程Ⅰ和过程Ⅱ中电场力做功分别为qU和－qU，电势能分别减少和增加qU，C正确；对于过程Ⅱ，重力势能减少，电势能增加，动能变化未知，D错误．

答案：AC

3. [2013·安徽联考]如图所示，六面体真空盒置于水平面上，它的ABCD面与EFGH面为金属板，其他面为绝缘材料．ABCD面带正电，EFGH面带负电．从小孔P沿水平方向以相同速度射入三个质量相同的带正电液滴A、B、C，最后分别落在1、2、3三点．则下列说法正确的是(　)

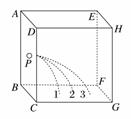
A．三个液滴在真空盒中都做平抛运动

B．三个液滴的运动时间不一定相同

C．三个液滴落到底板时的速率相同

D．液滴C所带电荷量最多

解析：三个液滴具有相同的水平初速度，但除了受重力以外，还受水平方向的电场力作用，不是平抛运动，选项A错误；在竖直方向上三个液滴都做自由落体运动，下落高度又相同，运动时间必相同，选项B错误；在相同的运动时间内，液滴C水平位移最大，说明它在水平方向的加速度最大，它受到的电场力最大，故它所带电荷量也最多，选项D正确；因为电场力对液滴C做功最多，它落到底板时的速率最大，选项C错误．

答案：D

2. 如图所示，质量为m的带正电滑块沿绝缘斜面匀加速下滑，当滑至竖直向下的匀强电场区域时，滑块的运动状态可能(　)

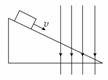
A．仍为匀加速下滑，加速度比原来的小

B．仍为匀加速下滑，加速度比原来的大

C．变成匀减速下滑，加速度和原来一样大

D．仍为匀加速下滑，加速度和原来一样大

解析：设斜面倾角为θ，滑块在开始下滑的过程中，mgsinθ－μmgcosθ＝ma，解得a＝gsinθ－μgcosθ>0，故sinθ>μcosθ.已知滑块带正电，(mg＋Eq)sinθ－μ(mg＋Eq)cosθ＝ma₁，a₁＝g(sinθ－μcosθ)＋(sinθ－μcosθ)，可推出加速度变大，选项B正确．

答案：B

1. 如图所示，平行板电容器与电源相连，下极板接地．一带电油滴位于两极板的中心P点且恰好处于静止状态，现将平行板电容器上极板迅速向下移动一些，则下列说法中正确的是(　)

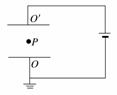
A. 带电油滴仍将保持静止状态

B. 带电油滴将向上做匀加速直线运动

C. 带电油滴将向下做匀加速直线运动

D. 带电油滴到达极板前电势能增大

解析：设原来两极板间距为d，两极板的电势差为U，带电油滴处于静止状态，则q＝mg.由于电容器始终与电源相连，两极板的电势差U保持不变，将平行板电容器上极板迅速向下移动一些，板间距离d减小，此时的电场力大于重力，则带电油滴将向上做匀加速直线运动，A、C两项错误，B项正确；油滴向上做初速度为零的匀加速直线运动，此过程中电场力做正功，油滴的电势能不断减小，D项错误．

答案：B

10. 如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、场区宽度为L.在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，磁感应强度B大小未知，圆形磁场区域半径为r.一质量为m、电荷量为q的带正电的粒子从A点由静止释放后，在M点离开电场，并沿半径方向射入磁场区域，然后从N点射出，O为圆心，∠MON＝120°，粒子重力可忽略不计．

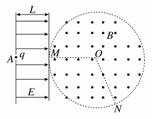
(1)求粒子经电场加速后，进入磁场时速度的大小；

(2)求匀强磁场的磁感应强度B的大小及粒子从A点出发到从N点离开磁场所经历的时间；

(3)若粒子在离开磁场前某时刻，磁感应强度方向不变，大小突然变为B′，此后粒子恰好被束缚在磁场中，则B′的最小值为多少？

解析：(1)设粒子经电场加速后的速度为v，根据动能定理有EqL＝mv²

解得：v＝

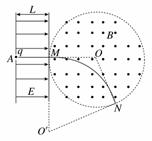
(2)粒子在磁场中完成了如图所示的部分圆运动，设其半径为R，因洛伦兹力提供向心力，

所以有qvB＝

由几何关系得＝tan30°

所以B＝

设粒子在电场中加速的时间为t₁，在磁场中偏转的时间为t₂

粒子在电场中运动的时间t₁＝＝

粒子在磁场中做匀速圆周运动，其周期为T＝＝

由于∠MON＝120°，所以∠MO′N＝60°

故粒子在磁场中运动时间t₂＝T＝

所以粒子从A点出发到从N点离开磁场所经历的时间：

t＝t₁＋t₂＝＋πr

(3)如图所示，当粒子运动到轨迹与OO′连线交点处改变磁场大小时，粒子运动的半径最大，即B′对应最小值

由几何关系得此时最大半径有R_m＝

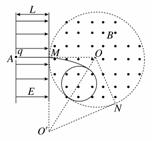
所以B′＝(＋1).

答案：(1)　(2)　＋πr　(3)(＋1)