4.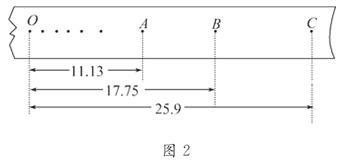（2010·许昌高一检测）（5分）在验证机械能守恒的实验中选出一条纸带如图2所示，以O为起始点，A、B、C三个计数点.打点计时器接通50 Hz的交流电，用最小刻度为毫米的刻度尺测得OA=11.13 cm、OB＝17.75 cm、OC＝25.9 cm.

这三个数据中不符合有效数字要求的是______，应该写成________cm，在计数点A和B，B和C之间还各有一个点，重锤的质量为m，根据以上数据，当振针打至B点时重锤的重力势能比开始下落时减少了______，这时它的动能增加了________.（g取9.80 m/s²）由此得出的结论是______________________.

3.（4分）在“验证机械能守恒定律”的实验中：

（1）将下列主要的实验步骤，按照实验的合理顺序把步骤前的序号填在题后横线上：

A.用手提着纸带使重物静止在靠近打点计时器处；

B.将纸带固定在重物上，让纸带穿过打点计时器的限位孔；

C.取下纸带，在纸带上任选几点，测出它们与第一个点的距离，并算出重物在打下这几个点时的瞬时速度；

D.接通电源，松开纸带，让重物自由下落；

E.查出当地的重力加速度g的值，算出打下各计数点时的动能和相应的减少的重力势能，比较它们是否相等；

F.把测量和计算得到的数据填入自己设计的表格里.

答：_______.

（2）动能值和相应重力势能的减少值相比，实际上哪个值应偏小些？

答：_______.

[解析]（1）实验的合理顺序应该是：BADCFE

（2）由于重物和纸带都受阻力作用，即都要克服阻力做功，所以有机械能损失，即重物的动能值要小于相应重力势能的减少值.

答案：（1）BADCFE　 （2）动能值

2.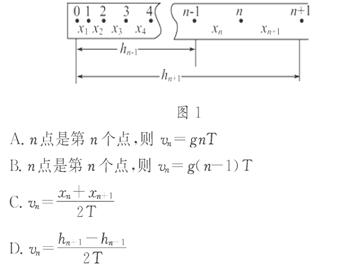（3分）如图1是用自由落体法验证机械能守恒定律时得到的一条纸带.有关尺寸在图中已注明.我们选中n点来验证机械能守恒定律.下面举一些计算n点速度的方法，其中正确的是(　 )

[解析]选C、D.v_n应表示从（n-1）到（n+1）间的平均速度.C、D对，A、B错.

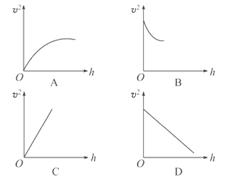
1.（3分）在验证机械能守恒定律的实验中，某同学依据纸带求得相关各点的瞬时速度以及与此相对应的下落距离h，以v2为纵轴，以h为横轴，建立坐标系，描点后画出变化图线，从而验证机械能守恒定律.若所有操作均正确，则得到的v2-h图象应是图中的（　 ）

7.9 实验：验证机械能守恒定律

[素能综合检测]

16. (14分)如图所示，第一象限的某个矩形区域内，有方向垂直纸面向外的匀强磁场B₁，磁场的下边界与x轴重合．一质量m＝1×10^－14kg、电荷量q＝1×10^－10C的带正电微粒以某一速度v沿与y轴负方向成60°角的方向从N点射入，经P点进入第四象限内沿直线运动，一段时间后，微粒经过y轴上的M点并沿与y轴负方向成60°角的方向飞出．第四象限内有互相正交的匀强电场E与匀强磁场B₂，E的大小为0.5×10³ V/m，B₂的大小为0.5 T；M点的坐标为(0，－10 cm)，N点的坐标为(0,30 cm)，不计微粒重力．

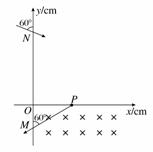
(1)求匀强磁场B₁的大小和微粒的运动速度v.

(2)B₁磁场区域的最小面积为多少？

解析：(1)带正电微粒以某一速度v沿与y轴负方向成60°角的方向从N点射入，由于重力忽略不计，微粒在第一象限内仅受洛伦兹力做匀速圆周运动；微粒在第四象限内仅受电场力和洛伦兹力，且微粒做直线运动，速度的变化会引起洛伦兹力的变化，所以微粒必做匀速直线运动，因此，电场力和洛伦兹力大小相等，方向相反，由力的平衡有Eq＝B₂qv

所以v＝＝ m/s＝1×10³ m/s

根据题意画出微粒的运动轨迹如图：

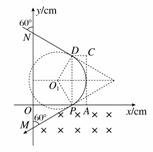
因为M点的坐标为(0，－10)，N点的坐标为(0,30)，由几何关系可知微粒在第一象限内做圆周运动的半径为

R＝ cm＝ m

微粒做圆周运动的向心力由洛伦兹力提供，即qB₁v＝m

解得B₁＝T.

(2)由图可知，磁场B₁的最小区域应该分布在图示的矩形PACD内．由几何关系易得

PD＝2Rsin60°＝0.2 m

PA＝R(1－cos60°)＝ m

所以，所求磁场的最小面积为

S＝PD·PA＝× m²＝ m².

答案：(1) T　1×10³ m/s　(2) m²

15. (12分)如图所示，水平放置的矩形容器内充满垂直纸面向外的匀强磁场，容器的高为d，右边足够宽，底面MN为荧光屏，在荧光屏中心O处置一粒子源，可以向纸面内以OA、OB为边界的区域内连续均匀发射速率为v₀、质量为m、电荷量为q的正粒子，其中沿OA方向发射的粒子刚好不碰到容器的上板面打在荧光屏上产生荧光．OA、OB与MN的夹角分别为α＝60°，β＝30°，不计粒子的重力及粒子间的相互作用．求：

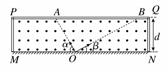
(1)磁场的磁感应强度B的大小；

(2)分别沿OA、OB方向发射的粒子在磁场中运动的时间差Δt.

解析：如图为粒子在匀强磁场中的运动轨迹．

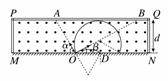
(1)设粒子源发出的粒子在磁场中运动的半径为r，对于沿OA方向发射的粒子，由几何关系得

r＋rsinβ＝d

解得r＝

由牛顿第二定律得Bqv₀＝

联立解得B＝

(2)沿OA、OB方向发射的粒子在磁场中运动的时间分别设为t₁、t₂，粒子做匀速圆周运动的周期设为T，则

T＝

t₁＝T

t₂＝T

Δt＝－T

联立解得Δt＝.

答案：(1)　(2)

14. (12分)如图所示，在xOy坐标平面的第一象限内存在有场强大小为E、方向竖直向上的匀强电场，第二象限内存在有方向垂直纸面向外的匀强磁场．荧光屏PQ垂直于x轴放置且距y轴的距离为L.一质量为m、带电荷量为＋q的粒子(不计重力)自坐标为(－L,0)的A点以大小为v₀、方向沿y轴正方向的速度进入磁场，粒子恰好能够到达原点O而不进入电场．现若使该带电粒子仍从A点进入磁场，但初速度大小为2v₀、方向与x轴正方向成45°角，求：

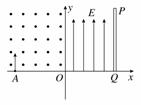
(1)带电粒子到达y轴时速度方向与y轴正方向之间的夹角．

(2)粒子最终打在荧光屏PQ上的位置坐标．

解析：(1)设磁场的磁感应强度为B，则由题意可知，当粒子以速度v₀进入磁场时，设其圆周运动的半径为R，有Bqv₀＝m，其中R＝

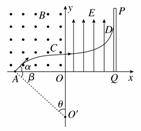
当粒子以初速度大小为2v₀、方向与x轴正方向成45°角进入磁场时，设其圆周运动的半径为R′，则有Bq2v₀＝m

由以上各式可解得R′＝L

由几何关系可知粒子做圆周运动的圆心在y轴上，所以该粒子必定垂直于y轴进入匀强电场．故粒子到达y轴时，速度方向与y轴正方向之间的夹角为90°.

(2)由几何关系可知CO＝(－1)L

带电粒子在电场中做类平抛运动，设其运动时间为t，在电场中向上运动的距离为h，则有：

L＝2v₀t，h＝at²，a＝

以上各式联立可解得：h＝

所以粒子最终打在荧光屏PQ上的位置坐标为

(L，＋(－1)L)

答案：(1)90°　(2)(L，＋(－1)L)

二、计算题

13. (12分)[2013·苏州模拟]如图所示为一电流表的原理示意图．质量为m的均质细金属棒MN的中点处通过一挂钩与一竖直悬挂的弹簧相连，绝缘弹簧劲度系数为k.在矩形区域abcd内有匀强磁场，磁感应强度大小为B，方向垂直纸面向外．与MN的右端N连接的一绝缘轻指针可指示标尺上的读数，MN的长度大于.当MN中没有电流通过且处于平衡状态时，MN与矩形区域的cd边重合，当MN中有电流通过时，指针示数可表示电流强度．

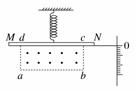
(1)当电流表示数为零时，弹簧伸长多少？(重力加速度为g)

(2)若要电流表正常工作，MN的哪一端应与电源正极相接？

(3)若k＝2.0 N/m，＝0.20 m，＝0.050 m，B＝0.20 T，此电流表的量程是多少？(不计通电时电流产生的磁场的作用)

(4)若将量程扩大2倍，磁感应强度应变为多大？

解析：(1)设当电流表示数为零时，弹簧的伸长量为Δx，则有mg＝kΔx，　①

解得：Δx＝.　②

(2)为使电流表正常工作，作用于通有电流的金属棒MN的安培力必须向下，因此M端应接正极．

(3)设电流表满偏时通过MN的电流强度为I_m，则有BI_m＋mg＝k(＋Δx)，　③

联立并代入数据得I_m＝2.5 A．　④

(4)设量程扩大后，磁感应强度变为B′，则有

2B′I_m＋mg＝k(＋Δx)．　⑤

解得：B′＝.　⑥

代入数据得：B′＝0.10 T.

答案：(1)　(2)M端　(3)2.5 A　(4)0.10 T

12. 如图所示，有一长方体金属块放在垂直表面C的匀强磁场中，磁感应强度大小为B，金属块的厚度为d，高为h，当有稳恒电流I沿平行平面C的方向通过金属块时，金属块上、下两面M、N上的电势分别为j_M、j_N，则下列说法中正确的是(　)

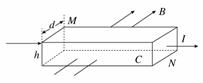
A. 由于磁场力的作用，金属块中单位体积内参与导电的自由电子数目为||

B. 由于磁场力的作用，金属块中单位体积内参与导电的自由电子数目为||

C. M面比N面电势高

D. 金属块的左面比右面电势低

解析：由于洛伦兹力作用使电子堆积在金属块上表面且形成一附加电场，方向向上．设两面M、N上的电势差为U，则U＝|j_M－j_N|，稳定时电子所受的洛伦兹力与电场力相平衡，则evB＝eU/h，根据金属导电时的规律I＝neSv，式中S＝dh，联立各式可得金属块中单位体积内参与导电的自由电子数目n＝||，选项A对，B错；由左手定则可知，电子积累在上端面，电势低，故C错；由于电源外的电路中电流由高电势流向低电势，故D错．

答案：A

第Ⅱ卷　(非选择题，共50分)