16．解：(1) (5分) 设绝缘棒与金属棒碰前的速率为v₁，绝缘棒在导轨由最低点向上滑动的过程中,由动能定理

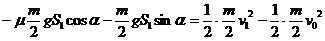　　 v₁=5m/s 　　　

（2）(10分）设碰后安培力对金属棒做功为W_安，由功能关系，安培力做的功等于回路中产生的总电热

　　　　 W_安= 0.25J　

　设碰后金属棒速率为v、切割磁感线产生的感应电动势为E，回路中感应电流为I，安培力为F_安

E=Bdv　　 　　　F_安=BId

由动能定理　　　　　 　

－W安－mgS2sinα－μmgS2cosα=0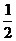－mv₂2　　 v=3m/s　

　设两棒碰后瞬时金属棒的加速度为a，由牛顿第二定律

　　 μmgcosα＋mgsinα＋F安= ma　　　 a = 25m/s2　

（3）（5分）设金属棒在导轨上运动时间为t，在此运动过程中，安培力的冲量为I_安，沿导轨方向，由动能定理

　　　 －I安－μmgtcosα－mgtsinα=0－mv　 …………………………………… (1分)　

　　 　I安=Bd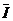△t　 　……………………………………………………… (1分)

由闭合电路欧姆定律　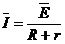　 　………………………………… (1分)

　由法拉第电磁感应定律　 　……………………………　 (1分)

　 得　　　　　　　 　　t = 0.2s　　 …………………………………　 (1分)

15．解：⑴设a的速度为v₁，由于b初态速度为零，则　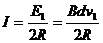 　①　 （2分）

　　　 对b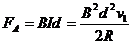：　②（2分）　　 　F_A＜mgsinθ　 ③（1分）

　　 将①②式代入③式得：v₁＜10m/s　 ④（2分）

⑵设a的速度为v₁，b的速度为v₂，回路电流为I，

则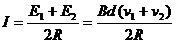：　 ⑤（1分）

对a：mgsinθ + F_A = F　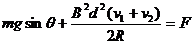 　⑥（2分

代入数据得: 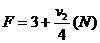　（1分）

设b的最大速度为v_m，则有：（2分） 代入数据得:　　 v_m= 8m/s

⑶对b：mgsinθ－F_A= ma　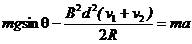 　（1分）

取任意无限小△t时间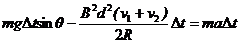：　 （2分）

代入数据并求和得：　 8t－x₂ = 2v₂　 （1分）

将t=2s，v₂=5.06m/s代入上式得：x₂=5.88m　 （1分）

a的位移：x₁=v₁t = 2×2 = 4m

由功能关系知：

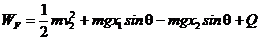　　 　（2分）

　　 代入数据得：W_F=14.9J　

14．(1)3:1　　　 (2)1: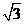　　 (3)2:1

13．(1) 根据安培力公式,推力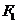=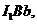其中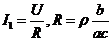

则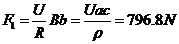

对海水推力的方向沿y轴方向(向右)

(2)

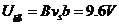
(3)根据欧姆定律,

安培推力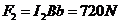

对船的推力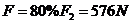

推力的功率

12．（1）根据磁场分布特点，线框不论转到磁场中哪一位置，切割磁感线的速度始终与磁场方向垂直，故线框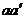转到图示位置时，感应电动势的大小E=2Blv=2Bl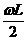=BlLω（3分）。

（2）线框转动过程中，只能有一个线框进入磁场（作电源），另一个线框与外接电阻R并联后一起作为外电路。.电源内阻为r，外电路总电阻R_外=r.故R两端的电压最大值：U_R=IR_外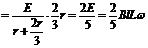（4分）

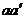（3）和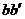在磁场中，通过R的电流大小相等，

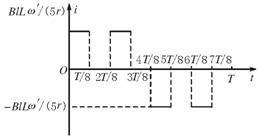
i_R=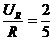BlLω·.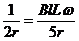

从线框aa′进入磁场开始计时，每隔T/8（线框转动45°）电流发生一次变化，其i_R随时间t变化的图象如图所示。（5分，其中图3分）

（4）因每个线框作为电源时产生的总电流和提供的功率分别为：

I=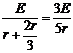,　P=IE=.（4分）

两线框转动一周时间内，上线圈只有两次进入磁场，每次在磁场内的时间（即作为电源时的做功时间）为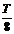.根据能的转化和守恒定律，外力驱动两线圈转动一周的功，完全转化为电源所获得的电能，所以

W_外=4P·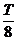=P·=P·（4分）

11．(1)运动。因磁场运动时，框与磁场有相对运动，ad、b边切害虫磁感线，框中产生感应电流(方向逆时针)，同时受安培力，方向水平向右，故使线框向右加速运动，且属于加速度越来越小的变加速运动。　　　 　　　 　　　 　　　 　　　 　　　 　 …………(6分)

(2)阻力f与安培力F安衡时，框有v_mf=Kv_m=F=2IBL①………(2分)

其中I=E/R 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　 ②………(1分)

E=2BL(v-v_m)　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　 ③………(2分)

①②③联立得：

Kv_m=2·[2BL(v-v_m)/R]·BL

∴Kv_m=(4B²L²v-4B²L²v_m)/R

∴v_m=4B²L²v/(KR+4B²L²) 　　　 　　　 　　　 　　　 　　　 　　　 ④………(1分)

　　 =3.2m/s　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 ⑤………(2分)

(3)框消耗的磁场能一部分转化为框中电热，一部分克服阴力做功。

据能量守恒

E_硫=I²Rt+Kv_m·v_mt　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 (4分)

E_磁=[4B²L²(v-v_m)²/R]·1+Kv_m²·1

　 =+018×3.2²

　 =2.9J　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 　　　 (2分)

v = －-----------

其中，v△t = △s--------------------------（1分）

在上升的全过程中

∑△v = －（gsinθ∑△t+B²L²∑△s/mR）

即　　　　　 0-v₀= －（t₀gsinθ+B²L²S/mR）-------------（1分）

∵H=S·sinθ　　　 且gsinθ= -------------------（1分）

∴　 H =（v₀²-gv₀t₀sinθ）/4g-----------------（1分）

10．第（1）问8分，第（2）问6分，第（3）问6分，共20分

解: （1）U型框向右运动时，NQ边相当于电源，产生的感应电动势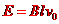　　　　　　　　　　　　　

　当如图乙所示位置时，方框bd之间的电阻为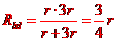　　

　U型框连同方框构成的闭合电路的总电阻为

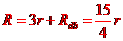
　闭合电路的总电流为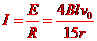　

　根据欧姆定律可知，bd两端的电势差为：　

　方框中的热功率为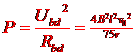　　　　

　 （2）在U型框向右运动的过程中，U型框和方框组成的系统所受外力为零，故系统动量守恒，设到达图示位置时具有共同的速度v，根据动量守恒定律

　　　解得：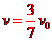　

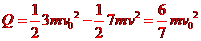　根据能量守恒定律，U型框和方框组成的系统损失的机械能等于在这一过程中两框架上产生的热量，即

　（3）设U型框和方框不再接触时方框速度为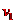，U型框的速度为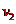，根据动量守恒定律，有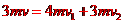　　　 　

两框架脱离以后分别以各自的速度做匀速运动，经过时间t方框最右侧和U型框最左侧距离为s，即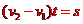

联立以上两式，解得：；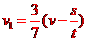　

a = －-----------------------

取一极短时间△t，速度微小变化为△v，由△v = a△t，得

4．5R＝gt²⑤

x₁＝v₁t＋R ⑥

由⑤⑥式解得x₁＝4R ⑦

当石块的质量为m时，设其到达管口C时速度大小为v₂，由机械能守恒定律有

E_p＝mg(1.5R＋R)＋v⑧

由④⑧式解得v₂＝2 ⑨

质量为m的石块落到水面上时，设离OO′的水平距离为x₂，则x₂＝v₂t＋R⑩

由⑤⑨⑩式解得x₂＝7R

石块能够落到水面的最大面积S＝(πx－πx)＝πR²(或8.25πR²)

18．答案：(1)　(2)3mgR

(3)πR²(或8.25πR²)

解析：(1)质量为m的石块到在管口C时做圆周运动的向心力完全由重力提供，则：mg＝m①

解得v₁＝②

(2)弹簧的弹性势能全部转化为石块的机械能，由机械能守恒定律有

E_p＝mg(1.5R＋R)＋mv ③

由②③式解得E_p＝3mgR ④

(3)不考虑因缓慢转动装置对石块速度大小的影响，质量为m的石块离开管口后做平抛运动，设经过t时间落到水面上，离OO′的水平距离为x₁，由平抛运动规律有