
47..(1)设导体杆在F的作用下运动至磁场的左边界时的速度为v1,根据动能定理则有 (F-μmg)s=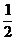 mv12
……2分
mv12
……2分
导体杆刚进入磁场时产生的感应电动势E=Blv1…………………………………1分
此时通过导体杆上的电流大小I=E/(R+r)=3.8A(或3.84A)………………2分
根据右手定则可知,电流方向为由b向a ………………………………………2分
(2)设导体杆在磁场中运动的时间为t,产生的感应电动势的平均值为E平均,则由法拉第电磁感应定律有 E平均=△φ/t=Bld/t…………………………………………………2分
通过电阻R的感应电流的平均值 I平均=E平均/(R+r)……………………………1分
通过电阻R的电荷量 q=I平均t=0.512C(或0.51C)………………………………2分
(3)设导体杆离开磁场时的速度大小为v2,运动到圆轨道最高点的速度为v3,因导体杆恰好能通过半圆形轨道的最高点,根据牛顿第二定律对导体杆在轨道最高点时有
mg=mv32/R0…………………………………………………………………………1分
对于导体杆从NN′运动至PP′的过程,根据机械能守恒定律有
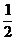 mv22=
mv22=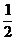 mv32+mg2R0………………………………………………………………1分
mv32+mg2R0………………………………………………………………1分
解得v2=5.0m/s…………………………………………………………………………1分
导体杆穿过磁场的过程中损失的机械能△E=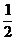 mv12-
mv12-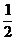 mv22=1.1J………………3分
mv22=1.1J………………3分
此过程中电路中产生的焦耳热为
Q=△E-μmgd=0.94J…………………………………………………………………2分
46. 解:(1)从图丙可以看出,线圈往返的每次运动都是匀速直线运动,其速度为
v==m/s=0.8 m/s ①……………………………………………(3分)
线圈做切割磁感线产生感生电动势E=nBLv ②………………………………… (2分)
L=2pr ③………………………………………………………(2分)
联立①②③式得E=nB2prv=20´0.2´2´3.14´0.1´0.8 ≈2 V ④………………(2分)
(2)感应电流 I== =0.2 A ⑤……………………………………(3分)
=0.2 A ⑤……………………………………(3分)
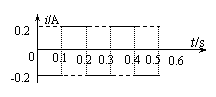 电流图像如右图 (2分)
电流图像如右图 (2分)
(3)由于线圈每次运动都是匀速直线运动,所以每次运动过程中推力必须等于安培力.
F推=F安=nBIL=2pnrBI=2´3.14´20´0.1´0.2´0.2 =0.5 N……………………(3分)
(4)发电机的输出功率即灯的电功率.P=I2R2=0.22´9.5=0.38W ……………(3分)
45. 解:(1)由法拉第电磁感应定律,两铜板间的电势差E=Blv0…………(2分)
由右手定则可判断出M板的电势高…………(2分)
(2)用电阻可忽略不计的导线将铜板M、N外侧相连接,即铜板由外侧短路后,M、N两板间的电动势E=Blv…………(2分)
短路电流I=E/R内,…………(1分)
R内=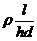 …………(3分)
…………(3分)
磁场对流体的作用力F=BIl…………(1分)
解得:F= …………(2分)
…………(2分)
方向与v方向相反(或水平向左)…………(1分)
(3)设流体在流动过程中所受的阻力与流速的比例系数为k,所以在外电路未短路时流体以稳定速度v0流过,此时流体所受的阻力(即涡轮机所提供的动力)F0=kv0……(1分)
此时涡轮机提供的功率P0=F0v0=kv02…………(1分)
外电路短路后,流体仍以稳定速度v0流过时,设此时磁场对流体的作用力为F磁,根据第(2)问的结果可知F磁=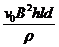 …………(1分)
…………(1分)
此时涡轮机提供的动力Ft=F0+F磁=kv0+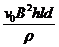 …………(1分)
…………(1分)
此时涡轮机提供的功率Pt=Fv0= kv02+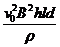 …………(1分)
…………(1分)
所以新增加功率△P=Pt-P0=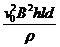 …………(1分)
…………(1分)
说明:第(3)问如果采用如下做法也得6分:
外电路没有接通,流体以稳定速度v0流过时,磁场对流体无作用力;外电路短路后,流体仍以稳定速度v0流过,设此时磁场对流体的作用力为F磁,外接涡轮机必须增加压力F用以平衡F磁,即 F=F磁…………(2分)
根据第(2)问的结果可知F磁= …………(2分)
…………(2分)
此时涡轮机新增加功率的功率△P =Fv0= 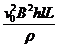 …………(2分)
…………(2分)
44.解:(1)由右手定则判断出感应电流的方向是abcda(或逆时针) 2分
缓冲车以速度 碰撞障碍物后滑块K静止,滑块相对磁场的速度大小为
碰撞障碍物后滑块K静止,滑块相对磁场的速度大小为 1分
1分
线圈中产生的感应电动势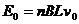 1分
1分
线圈中感应电流 1分
1分
解得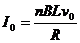 1分
1分
(2)设缓冲车的最大速度为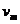 ,碰撞后滑块K静止,滑块相对磁场的速度大小为
,碰撞后滑块K静止,滑块相对磁场的速度大小为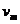 。
。
线圈中产生的感应电动势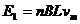 1分
1分
线圈中的电流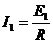 1分
1分
线圈ab边受到的安培力 2分
2分
依据牛顿第三定律,缓冲车厢受到的磁场力 1分
1分
依题意
解得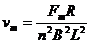 2分
2分
(3)设K、C碰撞后共同运动的速度为 ,由动量守恒定律
,由动量守恒定律
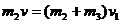 2分
2分
设缓冲车与物体C共同运动的速度为 2分
2分
由动量守恒定律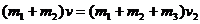 2分
2分
设线圈abcd产生的焦耳热为Q,依据能量守恒
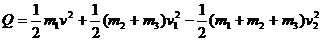
解得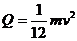 1分
1分
43. 解:(1)在运动过程中ab棒中的电流方向向左(b→a),cd棒受到的安培力方向垂直于纸面向里。 (2分)
(2)经过时间t,金属棒ab的速率 
此时,回路中的感应电流为 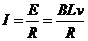
对金属棒ab,由牛顿第二定律得
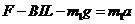
由以上各式整理得: 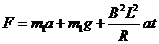 (1分)
(1分)
在图线上取两点:
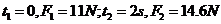 ,
,
代入上式得 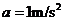 B=1.2T (2分)
B=1.2T (2分)
(3)在2s末金属棒ab的速率 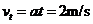
所发生的位移 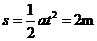 (1分)
(1分)
由动能定律得 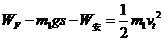 (1分)
(1分)
又 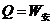
联立以上方程,解得
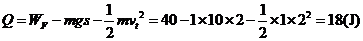 (1分)
(1分)
(4) cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大;后做加速度逐渐增大的减速运动,最后停止运动。 (2分)
当cd棒速度达到最大时,有 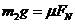
 又
又 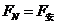
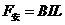
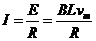
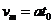
整理解得
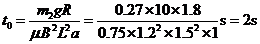 (2分)
(2分)
fcd随时间变化的图像如图(c)所示。 (2分)
42. 解:(1)(2分)因为电动势大小随时间均匀增大,根据E=BLv得速度v随时间均匀增大,线框作匀加速直线运动。 (2分)
(2)(5分)bc间电压U,则感应电动势4U/3
设线框边长l,则4U/3=Blv……① (2分)
Δt1时间内,平均感应电动势E=Δφ/Δt1=Bl2/Δt1……② (2分)
联立得E=16U2/(9Bv2Δt1) (1分)
(3)(6分)设线框加速度a,bc边进入磁场时速度v,Δt1=Δt2=2Δt3=2Δt,线框边长l,磁场宽L
根据三段时间内线框位移,得

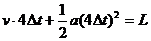
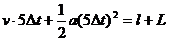 (4分)
(4分)
解得l/L=7∶18 (2分)
(4)(3分)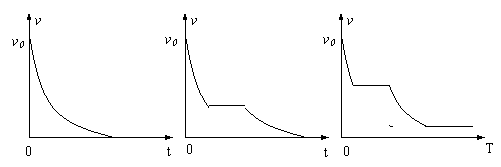
41. 解:(1)设ab棒离开磁场边界前做匀速运动的速度为v,产生的电动势为E = BLv (1分)
电路中电流 I = 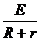 (1分)
(1分)
对ab棒,由平衡条件得 mg-BIL = 0 (1分)
解得 v = 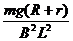 (2分)
(2分)
(2) 由能量守恒定律:mg(d0 + d) = E电 + 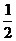 mv2
(1分)
mv2
(1分)
解得 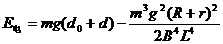 (2分)
(2分)
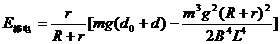 (2分)
(2分)
(3)设棒自由落体d0高度历时为t0,由d0 = 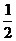 gt02,得t0 =
gt02,得t0 = 
棒在磁场中匀速时速度为v = 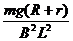 ,设
,设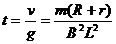
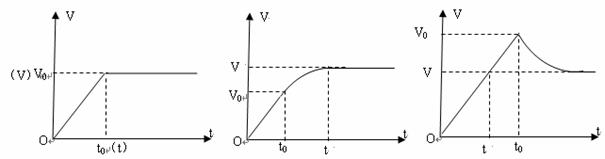
1 当t0=t,即d0 = 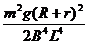 时,棒进入磁场后做匀速直线运
时,棒进入磁场后做匀速直线运
2 当t0 < t,即d0 <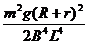 时,棒进入磁场后做先加速后匀速直线运动
时,棒进入磁场后做先加速后匀速直线运动
3 当t0>t,即d0>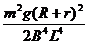 时,棒进入磁场后做先减速后匀速直线运动
时,棒进入磁场后做先减速后匀速直线运动
40. 解:(1)通过cd棒的电流方向 d→c(1分)
区域I内磁场方向为垂直于斜面向上(1分)
(2)对cd棒,F安=BIl=mgsinθ所以通过cd棒的电流大小I = (1分)
当ab棒在区域II内运动时cd棒消耗的电功率P=I2R=(1分)
(3)ab棒在到达区域II前做匀加速直线运动,a==gsinθ
cd棒始终静止不动,ab棒在到达区域II前、后,回路中产生的感应电动势不变,则ab棒在区域II中一定做匀速直线运动
可得;=Blvt =Blgsinθt x 所以t x=(2分)
ab棒在区域II中做匀速直线运动的速度vt=
则ab棒开始下滑的位置离EF的距离h= a t x2+2l=3 l(3分)
(4) ab棒在区域II中运动的时间t2==(1分)
ab棒从开始下滑至EF的总时间t= t x+t2=2 ε=Blvt =Bl(2分)
ab棒从开始下滑至EF的过程中闭合回路中产生的热量:Q=εIt=4mglsinθ(2分
39. 解:(1)当金属棒匀速运动时,
进入磁场前,
进入磁场后,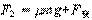
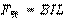
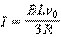
解得: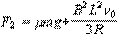
(2)金属棒在磁场外运动过程中,
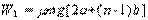
穿过 n 段磁场过程中,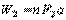
所以拉力做功为:
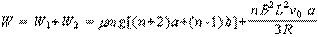
(3)金属棒进入磁场前,
穿过第一段磁场过程中,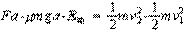 金属棒从穿出第一段磁场到进入第二段磁场的过程中,
金属棒从穿出第一段磁场到进入第二段磁场的过程中,
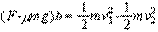
整个过程中电阻上产生的总热量为:
解得: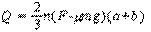
38.解:(1)k接到W#W$W%.K**S*&5^U1位置时

 ,
,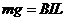 ,
, 
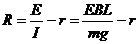
(2)k接到2位置时, ,
,
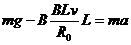 ,
,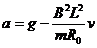

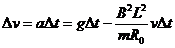


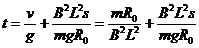
(3)k接到3位置时,ab棒做匀加速运动

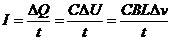
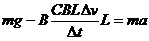
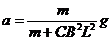
设下落距离s时的速度为v
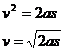
此时电容器储存的电能为E
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com