16. (18分)　 如图，简谐横波在t时刻的波形如实线所示，经过Δt＝3 s，其波形如虚线所示．已知图中x₁与x₂相距1 m，波的周期为T，且2T<Δt<4T.则

(1)可能的最小波速为多少？

(2)最小周期为多少？

解析：由波形图可知波长为λ＝7 m，所以Δx＝1 m＝

λ，所以Δt＝(n＋)T或Δt＝(n＋)T，又由于2T<Δt<4T，所以周期的最大可能值为T_max＝ s＝1.4 s，周期的最小可能值为T_min＝ s＝ s，可能的最小波速为v_min＝＝ m/s＝5 m/s.

答案：(1)5 m/s　(2) s

三、计算题

14. (10分)如图所示，实线为一简谐波该时刻的波形图，虚线是该波经0.2 s后的波形图．

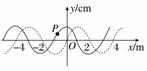
(1)若波向左传播，指出此时刻P点的振动方向并求出经0.2 s后波传播的距离；

(2)若波向右传播，求它的最大周期；

(3)若波速是35 m/s，求波的传播方向．

解析：根据波的图象和传播方向通过“带动法”或“微平移法”可得P点的振动方向；根据两个时刻的波形图可得其在0.2 s内传播的距离，根据时空的对应性可得该波周期的通式．

(1)若波向左传播，在图中实线波形图对应的时刻P点向上振动

由图可知经0.2 s后波传播的距离为x＝(3＋4n)m(n＝0,1,2，…)

(2)若波向右传播，则实线波形图到虚线波形图所经过的时间t＝＋nT(n＝0,1,2，…)，当n＝0时周期有最大值T_max＝4t＝0.8 s

(3)若波速为35 m/s，则0.2 s内波传播的距离为x＝vt＝7.0 m，而λ＝4 m，故x＝1λ，故波向左传播．

答案：(1)见解析　(2)0.8 s　(3)向左传播

13. (8分)实验室有一块长方体透明介质，截面如图中ABCD所示．AB的长度为l₁，AD的长度为l₂，且AB和AD边透光，而BC和CD边不透光，且射到这两个边的光线均被全部吸收．现让一平行光束以入射角θ₁射到AB面上，经折射后AD面上有光线射出，甲、乙两同学分别用不同方法测量该长方体介质的折射率．

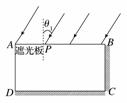
　(1)甲同学的做法是：保持射到AB面上光线的入射角不变，用遮光板由A点沿AB缓慢推进，遮光板前端推到P时，AD面上恰好无光线射出，测得AP的长度为l₃，则长方体介质的折射率可表示为n＝________.

(2)乙同学的做法是：缓慢调节射到AB上光线的入射角，使AD面也恰好无光线射出，测得此时射到AB面上光线的入射角为θ₂，则长方体介质的折射率可表示为n＝________.

(3)θ₁和θ₂的关系为：θ₁________θ₂(填“<”、“>”或“＝”)．

解析：(1)由题意可知，过P点入射光线的折射光线恰好过D点，设此时折射角为γ₁，则

sinγ₁＝，n＝＝.

(2)由题意可知，射到AD面上的光线在AD面上恰好发生全反射，设在AB面上的折射角为γ₂，则在AD面上的入射角为临界角，且C＝90°－γ₂，由n＝＝解得：

n＝.

(3)因为在AB面的折射角越小，在AD面的入射角越大，而在AB面入射角越小，折射角越小，故应减小AB面的入射角才能使光线在AD面发生全发射，因此θ₁>θ₂.

答案：(1)　(2)　(3)>

12. (8分)有两个同学利用假期分别去参观北大和南大的物理实验室，各自利用先进的DIS系统较准确地探究了“单摆的周期T与摆长L的关系”，他们通过校园网交换了实验数据，并由计算机绘制了T²－L图象，如图甲所示．去北大的同学所测实验结果对应的图线是________(选填“A”或“B”)．另外，在南大做探究的同学还利用计算机绘制了两种单摆的振动图象(如图乙)，由图可知，两单摆摆长之比＝________.

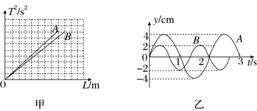
解析：由T＝2π得，T²＝L，根据图甲可知＞，即g_A＜g_B，因北大更靠近北极，其所在地的重力加速度更大些，应选B；根据图甲可知＝·＝＝，由图乙可得＝，由T²＝L得，＝＝2.

答案：B　2

二、填空题

11.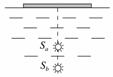 (6分)　　 如图所示，平静的水面下同一竖直线上有两个点光源S_a、S_b，可分别发出a、b两种不同颜色的单色光．在光源的正上方放置一个圆形的遮光板，在水面上方同时恰好看不到两个光源．则a光的频率________(选填“>”、“＝”或“<”，下同)b光的频率；若用同一装置做杨氏双缝干涉实验，a光的干涉条纹宽度________b光的干涉条纹宽度．

解析：　　　 由题意可知a光的临界角大于b光的临界角，根据折射率与临界角的关系可知水对a光的折射率小于水对b光的折射率，根据频率与折射率的关系可知a光的频率小于b光的频率．根据波速公式可知a光在真空中的波长大于b光在真空中的波长，根据n＝可知a光在水中的波长大于b光在水中的波长，若用同一装置做杨氏双缝干涉实验，a光的干涉条纹宽度大于b光的干涉条纹宽度．

答案：<　>

9. 如图，一玻璃柱体的横截面为半圆形，一单色细光束从空气射向柱体的O点(半圆的圆心)，产生反射光束1和折射光束2，已知玻璃的折射率为，入射角为45°，现保持入射光不变，将半圆柱绕通过O点且垂直于图面的轴顺时针转过15°，如图中虚线所示，则(　)

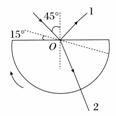
A. 光束1顺时针转过15°

B. 光束1顺时针转过30°

C. 光束2顺时针转过的角度小于15°

D. 光束2顺时针转过的角度大于15°

解析：当圆柱转过15°时，入射角变为60°，则反射角也变为60°，故光束1顺时针转过30°；折射角的改变量小于入射角的改变量，故光束2顺时针转过的角度小于15°.

答案：BC

8. [2014·天津河西区期末]　　　　 一列简谐横波沿x轴负方向传播，a、b为波上的两个质点，某时刻的波形图如图甲所示，从此时刻开始计时，图乙是a、b两个质点中某一质点的振动图象，下列判断正确的是　　 (　 　 )

A. 波速为1.0 m/s，图乙是质点a的振动图象

B. 波速为1.0 m/s，图乙是质点b的振动图象

C. 波速为0.16 m/s，图乙是质点a的振动图象

D. 波速为0.16 m/s，图乙是质点b的振动图象

解析：由图甲可知机械波的波长λ＝0.4 m，由图乙可知质点振动周期T＝0.4 s，则波速v＝＝ m/s＝1.0 m/s.根据波的传播规律与质点振动之间的关系可知，该时刻质点a向下振动，质点b向上振动，因此图乙是质点b的振动图象，B正确．

答案：B

17. (10分)如图所示，在MN的下方足够大的空间是玻璃介质，其折射率为n＝，玻璃介质的上边界MN是屏幕．玻璃中有一正三角形空气泡，其边长l＝40 cm，顶点与屏幕接触于C点，底边AB与屏幕平行．激光a垂直于AB边射向AC边的中点O，结果在屏幕MN上出现两个光斑．

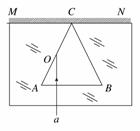
(1)画出光路图；

(2)求两个光斑之间的距离L.

解析：(1)画出光路示意图如图所示

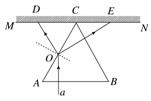
(2)在界面AC，a光的入射角θ₁＝60°

由光的折射定律得：

＝n

代入数据求得折射角

θ₂＝30°

由光的反射定律得反射角θ₃＝60°

由几何关系易得：△ODC是边长为l/2的正三角形，△COE为等腰三角形，CE＝OC＝l/2

故两光斑之间的距离L＝DC＋CE＝l＝40 cm.

答案：(1)见解析图　(2)40 cm

A. P光束只有蓝光　　　　　　　　　　　　　　　　　　 B. P光束只有红光

C. Q光束只有蓝光　　　　　　　　　　　　　　　　　　 D. Q光束只有红光

解析：蓝光折射率大，易发生全反射，由图可知，只有一条折射光线，说明蓝光发生了全反射，Q光束只有红光；有折射就有反射，P光束为红光和蓝光组成的复色光．

答案：D

16. (18分)　 如图，简谐横波在t时刻的波形如实线所示，经过Δt＝3 s，其波形如虚线所示．已知图中x₁与x₂相距1 m，波的周期为T，且2T<Δt<4T.则

(1)可能的最小波速为多少？

(2)最小周期为多少？

解析：由波形图可知波长为λ＝7 m，所以Δx＝1 m＝

λ，所以Δt＝(n＋)T或Δt＝(n＋)T，又由于2T<Δt<4T，所以周期的最大可能值为T_max＝ s＝1.4 s，周期的最小可能值为T_min＝ s＝ s，可能的最小波速为v_min＝＝ m/s＝5 m/s.

答案：(1)5 m/s　(2) s

15. (10分)如图所示，一透明球体置于空气中，球半径R＝10 cm，折射率n＝.MN是一条通过球心的直线，单色细光束沿直线AB且平行于MN射向球体，B点为入射点，AB与MN间距为5 cm，出射光线沿CD方向．

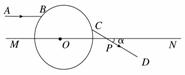
(1)补全光路并求出光从B点传到C点的时间；

(2)求CD与MN所成的角α.(需写出求解过程)

解析：(1)连接BC，如图所示，设B点光线的入射角、折射角分别标为i、r，由几何关系可知

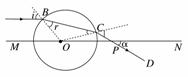
sini＝/2，所以i＝45°

对B点应用折射定律得n＝

sinr＝1/2，故r＝30°

BC＝2Rcosr

t＝nBC/c＝2nRcosr/c

解得t＝(/3)×10^－9 s

(2)由几何关系可知∠COP＝15°，∠OCP＝135°，α＝30°.

答案：(1)图见解析　(2)(/3)×10^－9 s　(2)30°