
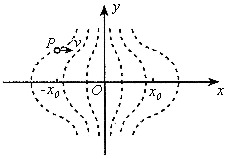
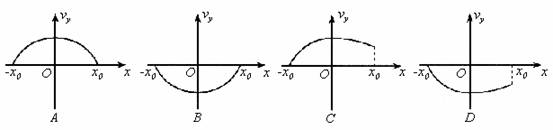
28. (04北京理综) 静电透镜是利用静电场使电子束会聚或发散的一种装置,其中某部分静电场的分布如下图所示。虚线表示这个静电场在xoy平面内的一簇等势线,等势线形状相对于ox轴、oy轴对称。等势线的电势沿x轴正向增加,且相邻两等势线的电势差相等。一个电子经过P点(其横坐标为-x0)时,速度与ox轴平行。适当控制实验条件,使该电子通过电场区域时仅在ox轴上方运动。在通过电场区域过程中,该电子沿y方向的分速度vy随位置坐标x变化的示意图是
25.[命题意图]本题考查万有引力定律的应用及单摆的周期公式,意在考查对基本物理规律的分析计算能力。
解:在地面处,单摆所受万有引力近似等于其重力,即 ,
,
单摆的在地面的摆动周期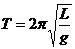
设地球密度为ρ,地球的体积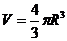 ,
,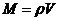
综合以上四得得: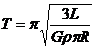
同理可知,矿井内单摆的周期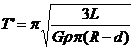
而单摆在地面处的摆动周期与矿井底部摆动周期之比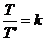
解得:
五.万有引力与航天
(2012上海)22B.人造地球卫星做半径为r,线速度大小为v的匀速圆周运动。当其角速度变为原来的倍后,运动半径为_________,线速度大小为_________。
22B.[考点]本题考查万有引力在天体运动中的应用
[解析]由 可知,角速度变为原来的倍后,半径变为2r,由
可知,角速度变为原来的倍后,半径变为2r,由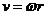 可知,角速度变为原来的倍后,线速度大小为v。
可知,角速度变为原来的倍后,线速度大小为v。
[答案]2r,v
(2012新课标)21假设地球是一半径为R.质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。矿井底部和地面处的重力加速度大小之比为
A.1- B.1+ C.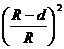 D
.
D
.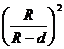
21[答案]A
在地球表面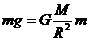 ,又
,又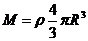 ,所以
,所以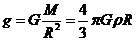 ,因为球壳对球内物体的引力为零,所以在深为d的矿井内
,因为球壳对球内物体的引力为零,所以在深为d的矿井内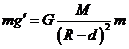 ,得
,得 ,所以
,所以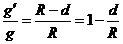 。
。
25.(2012 大纲卷)一单摆在地面处的摆动周期与在某矿井底部摆动周期的比值为k。设地球的半径为R。假定地球的密度均匀。已知质量均匀分布的球壳对壳内物体的引力为零,求矿井的深度d。
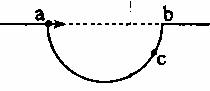
13.(2012海南卷),如图,水平地面上有一个坑,其竖直截面为半圆。ab为沿水平方向的直径。若在a点以初速度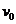 沿ab方向抛出一小球,
小球会击中坑壁上的c点。已知c点与水平地面的距离为圆半径的一半,求圆的半径。
沿ab方向抛出一小球,
小球会击中坑壁上的c点。已知c点与水平地面的距离为圆半径的一半,求圆的半径。
解析:设圆半径为r,质点做平抛运动,则:
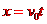 ①
①
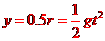 ②
②
过c点做cd⊥ab与d点,Rt△acd∽Rt△cbd可得 即为:
即为:
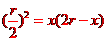 ③
③
由①②③得: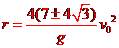
12.(2012福建卷).(15分)
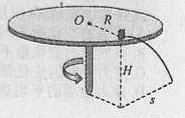 如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动。现测得转台半径R=0.5 m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m。设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2
求:
如图,置于圆形水平转台边缘的小物块随转台加速转动,当转速达到某一数值时,物块恰好滑离转台开始做平抛运动。现测得转台半径R=0.5 m,离水平地面的高度H=0.8m,物块平抛落地过程水平位移的大小s=0.4m。设物块所受的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2
求:
(1)物块做平抛运动的初速度大小V0;
(2)物块与转台间的动摩擦因数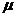 。
。
答案:

11.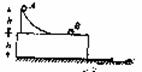 (2012天津卷).如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面高也为h,坡道底端与台面相切。小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半,两球均可视为质点,忽略空气阻力,重力加速度为g,求
(2012天津卷).如图所示,水平地面上固定有高为h的平台,台面上有固定的光滑坡道,坡道顶端距台面高也为h,坡道底端与台面相切。小球A从坡道顶端由静止开始滑下,到达水平光滑的台面后与静止在台面上的小球B发生碰撞,并粘连在一起,共同沿台面滑行并从台面边缘飞出,落地点与飞出点的水平距离恰好为台高的一半,两球均可视为质点,忽略空气阻力,重力加速度为g,求
(1)小球A刚滑至水平台面的速度vA;
(2)A、B两球的质量之比mA:mB
.(16分)
解析:(1)小球A在坡道上只有重力做功机械能守恒,有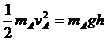 ①
①
解得
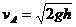 ②
②
(2)小球A、B在光滑台面上发生碰撞粘在一起速度为v,根据系统动量守恒得
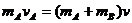 ③
③
离开平台后做平抛运动,在竖直方向有 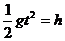 ④
④
在水平方向有  ⑤
⑤
联立②③④⑤化简得 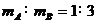
10.(2012浙江卷).由光滑细管组成的轨道如图所示,其中AB段和BC段是半径为R的四分之一圆弧,轨道固定在竖直平面内。一质量为m的小球,从距离水平地面为H的管口D处静止释放,最后能够从A端水平抛出落到地面上。下列说法正确的是( )
A.小球落到地面时相对于A点的水平位移值为
 B. 小球落到地面时相对于A点的水平位移值为
B. 小球落到地面时相对于A点的水平位移值为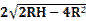
C.小球能从细管A端水平抛出的条件是H>2R
D.小球能从细管A端水平抛出的最小高度Hmin= 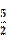 R
R
答案:BC
9.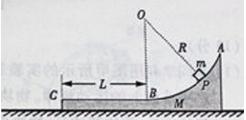 (2012山东卷).(15分)如图所示,一工件置于水平地面上,其AB段为一半径
(2012山东卷).(15分)如图所示,一工件置于水平地面上,其AB段为一半径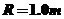 的光滑圆弧轨道,BC段为一长度
的光滑圆弧轨道,BC段为一长度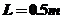 的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量
的粗糙水平轨道,二者相切与B点,整个轨道位于同一竖直平面内,P点为圆弧轨道上的一个确定点。一可视为质点的物块,其质量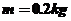 ,与BC 间的动摩擦因数
,与BC 间的动摩擦因数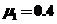 。工件质
。工件质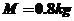 ,与地面间的动摩擦因数
,与地面间的动摩擦因数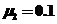 。(取
。(取
(1)若工件固定,将物块由P点无初速度释放,滑至C点时恰好静止,求P、C两点间的高度差h。
(2)若将一水平恒力F作用于工件,使物体在P点与工件保持相对静止,一起向左做匀加速直线运动
1求F的大小
2当速度时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离。
(1)物块从P点下滑经B点至C点的整个过程,根据动能定理得
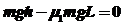
代入数据得
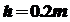 2
2
(2)1设物块的加速度大小为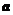 ,P点与圆心的连线与竖直方向间的夹角为
,P点与圆心的连线与竖直方向间的夹角为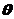 ,由几何关系可得
,由几何关系可得
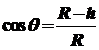 3
3
根据牛顿第二定律,对物体有
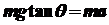 4
4
对工件和物体整体有
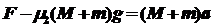 5
5
联立2345式,代入数据得
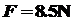 6
6
2设物体平抛运动的时间为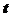 ,水平位移为
,水平位移为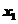 ,物块落点与B间的距离为
,物块落点与B间的距离为  , 由运动学公式可得
, 由运动学公式可得
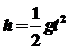 7
7
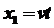 8
8
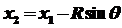 9
9
联立2378 9式,代入数据得
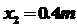 10
10
8.(2012北京高考卷).(16分)
如图所示,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度υ飞离桌面,最终落在水平地面上.已知l=1.4m,υ=3.0 m/s,m=0.10kg,物块与桌面间的动摩擦因数μ=0.25,桌面高h=0.45m,不计空气阻力,重力加速度g取10m/s2.求:
 (1)小物块落地点距飞出点的水平距离s;
(1)小物块落地点距飞出点的水平距离s;
(2)小物块落地时的动能Ek;
(3)小物块的初速度大小υ0.
(16分)
(1)由平抛运动规律,有
竖直方向
h=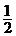 gt2
gt2
水平方向 s=υt
得水平距离
s=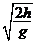 υ=0.90m
υ=0.90m
(2)由机械能守恒定律,动能 Ek=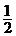 mυ2+mgh=0.90J
mυ2+mgh=0.90J
(3)由动能定理,有
-μmg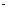 l=
l=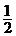 mυ2-
mυ2-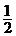 mυ02
mυ02
得初速度大小
υ0=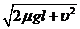 =4.0m/s
=4.0m/s
7.(2012全国理综).(20分)
一探险队员在探险时遇到一山沟,山沟的一侧竖直,另一侧的坡面呈抛物线形状。此队员从山沟的竖直一侧,以速度v0沿水平方向跳向另一侧坡面。如图所示,以沟底的O点为原点建立坐标系Oxy。已知,山沟竖直一侧的高度为2h,坡面的抛物线方程为y=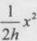 ,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。
,探险队员的质量为m。人视为质点,忽略空气阻力,重力加速度为g。
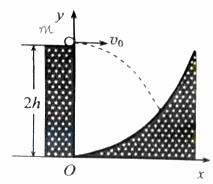
(1) 求此人落到破面试的动能;
(2) 此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少?
[解析]
(1)
平抛运动的分解: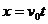 ,
,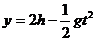 ,得平抛运动的轨迹方程
,得平抛运动的轨迹方程 ,此方程与坡面的抛物线方程为y=
,此方程与坡面的抛物线方程为y=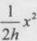 的交点为
的交点为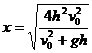 ,
,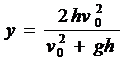 。
。
根据机械能守恒,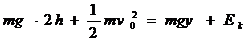
解得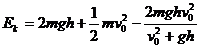
(3)
(2)求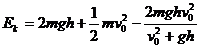 关于
关于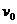 的导数并令其等于0,解得当此人水平跳出的速度为
的导数并令其等于0,解得当此人水平跳出的速度为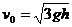 时,他落在坡面时的动能最小,动能的最小值为
时,他落在坡面时的动能最小,动能的最小值为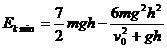 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com