
 (2)空间向量基本定理:如果三个向量
(2)空间向量基本定理:如果三个向量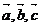 不共面,那么对空间任一向量
不共面,那么对空间任一向量 ,存在一个唯一的有序实数组x、y、z,使
,存在一个唯一的有序实数组x、y、z,使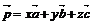 .
.
10. 空间向量.
(1)a.共线向量:共线向量亦称平行向量,指空间向量的有向线段所在直线互相平行或重合.
9. 平面平行与平面垂直.
(1)空间两个平面的位置关系:相交、平行.
(2)平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,哪么这两个平面平行.(“线面平行,面面平行”)
推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.
(3)两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行,线线平行”)
(4)两个平面垂直性质判定一:两个平面所成的二面角是直二面角,则两个平面垂直.
两个平面垂直性质判定二:如果一个平面与一条直线垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直,面面垂直”)
(5)两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.
8. 直线与平面平行、直线与平面垂直.
(1)空间直线与平面位置分三种:相交、平行、在平面内.
(2)直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)
(3)直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)
(4)直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.
直线与平面垂直判定定理:如果一条直线和一个平面内的两条相交直线垂直,则这条直线与这个平面垂直。
推论:如果两条直线同垂直于一个平面,那么这两条直线平行.
7. 空间直线.
(1)空间直线位置分三种:相交、平行、异面. 相交直线―共面有且有一个公共点;平行直线―共面没有公共点;异面直线―不同在任一平面内。
(2)异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)
(3)平行公理:平行于同一条直线的两条直线互相平行.
(4)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.
6.平面
(1)对平面的理解
平面是一个不加定义、只须理解的最基本的原始概念.
立体几何中的平面是理想的、绝对平且无限延展的模型,平面是无大小、厚薄之分的.类似于我们以前学的直线,它可以无限延伸,它是不可度量的.
(2)对公理的剖析
(1)公理1的内容反映了直线与平面的位置关系,公理1的条件“线上不重合的两点在平面内”是公理的必要条件,结论是“线上所有点都在面内”.这个结论阐述了两个观点:一是整条直线在平面内;二是直线上所有点在平面内.
其作用是:可判定直线是否在平面内、点是否在平面内.
(2)公理2中的“有且只有一个”的含义要准确理解.这里的“有”是说图形存在,“只有一个”是说图形唯一,确定一个平面中的“确定”是“有且只有”的同义词,也是指存在性和唯一性这两方面.这个术语今后也会常常出现,要理解好.
其作用是:一是确定平面;二是证明点、线共面.
(3)公理3的内容反映了平面与平面的位置关系,它的条件简而言之是“两面共一点”,结论是“两面共一线,且过这一点,线唯一”.对于本公理应强调对于不重合的两个平面,只要它们有公共点,它们就是相交的位置关系,交集是一条直线.
其作用是:其一它是判定两个平面是否相交的依据,只要两个平面有一个公共点,就可以判定这两个平面必相交于过这点的一条直线;其二它可以判定点在直线上,点是两个平面的公共点,线是这两个平面的公共交线,则这点在交线上.
(3)已知图形中平行于x轴、y轴或z轴的线段,在直观图中分别画成平行于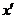 轴、
轴、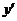 轴和
轴和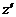 轴的线段.
轴的线段.
(4)已知图形中平行于x轴和z轴的线段,在直观图中长度相等;平行于y轴的线段,长度取一半.
(2)画直观图时把它们画成对应的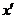 轴、
轴、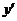 轴和
轴和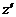 轴,它们相交于
轴,它们相交于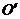 ,并使
,并使 45°,
45°, 90°。
90°。
(1)在空间图形中取互相垂直的x轴和y轴,两轴交于O点,再取z轴,使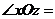 90°,且
90°,且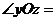 90°.
90°.
5、直观图画法
斜二测画法的规则:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com