一、选择题

1、在1，0，2，-3这四个数中，最大的数是（　　 ）

　 A、1　　　　　　　 B、0　　　　　　 C、2　　　　 D、-3

29．（2014•台湾）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE．请完整说明为何△ABC与△DEC全等的理由．

解：∵∠BCE=∠ACD=90°， ∴∠3+∠4=∠4+∠5， ∴∠3=∠5， 在△ACD中，∠ACD=90°， ∴∠2+∠D=90°， ∵∠BAE=∠1+∠2=90°， ∴∠1=∠D， 在△ABC和△DEC中， ， ∴△ABC≌△DEC（AAS）．

二、非选择题

28．（2014•台湾）已知甲校有a人，其中男生占60%；乙校有b人，其中男生占50%．今将甲、乙两校合并后，小清认为：「因为=55%，所以合并后的男生占总人数的55%．」如果是你，你会怎么列式求出合并后男生在总人数中占的百分比？你认为小清的答案在任何情况都对吗？请指出你认为小清的答案会对的情况．请依据你的列式检验你指出的情况下小清的答案会对的理由．

　解析：合并后男生在总人数中占的百分比是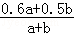：×100%．

当a=b时小清的答案才成立；

当a=b时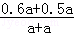，×100%=55%．

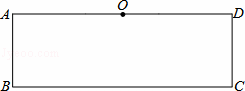
27．（3分）（2014•台湾）如图，矩形ABCD中，AD=3AB，O为AD中点，是半圆．甲、乙两人想在上取一点P，使得△PBC的面积等于矩形ABCD的面积其作法如下：

（甲） 延长BO交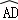于P点，则P即为所求；

（乙） 以A为圆心，AB长为半径画弧，交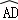于P点，则P即为所求．

对于甲、乙两人的作法，下列判断何者正确？（　）

解析：　　 解：要使得△PBC的面积等于矩形ABCD的面积，

需P_甲H=P_乙K=2AB．

故两人皆错误．

故选：B．

26．已知a、h、k为三数，且二次函数y=a（x﹣h）²+k在坐标平面上的图形通过（0，5）、（10，8）两点．若a＜0，0＜h＜10，则h之值可能为下列何者？（　）

解析：　　 解：∵抛物线的对称轴为直线x=h，

而（0，5）、（10，8）两点在抛物线上，

∴h﹣0＞10﹣h，解得h＞5．

故选D．

25．有甲、乙两个箱子，其中甲箱内有98颗球，分别标记号码1～98，且号码为不重复的整数，乙箱内没有球．已知小育从甲箱内拿出49颗球放入乙箱后，乙箱内球的号码的中位数为40．若此时甲箱内有a颗球的号码小于40，有b颗球的号码大于40，则关于a、b之值，下列何者正确？（　）

解析：　　 甲箱98﹣49=49（颗），

∵乙箱中位数40，

∴小于、大于40各有（49﹣1）÷2=24（颗），

∴甲箱中小于40的球有39﹣24=15（颗），大于40的有49﹣15=34（颗），即a=15，b=34．

故选D

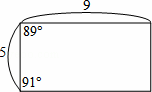
24．下列选项中的四边形只有一个为平行四边形，根据图中所给的边长长度及角度，判断哪一个为平行四边形？（　）

A．

B．

C．

D．

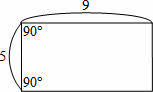解析：　　 （A） 上、下这一组对边平行，可能为等腰梯形；

（B） 上、下这一组对边平行，可能为等腰梯形，但此等腰梯形底角为90°，所以为平行

四边形；

（C） 上、下这一组对边平行，可能为梯形；

（D） 上、下这一组对边平行，可能为梯形；

故选B

23．若有一等差数列，前九项和为54，且第一项、第四项、第七项的和为36，则此等差数列的公差为何？（　）

解析：　　 ∵前九项和为54，

∴第五项=54÷9=6，

∵第一项、第四项、第七项的和为36，

∴第四项=36÷3=12，

∴公差=第五项﹣第四项=6﹣12=﹣6．　　

故选：A

22．图为歌神KTV的两种计费方案说明．若晓莉和朋友们打算在此KTV的一间包厢里连续欢唱6小时，经服务生试算后，告知他们选择包厢计费方案会比人数计费方案便宜，则他们至少有多少人在同一间包厢里欢唱？（　）

解析：　　 设晓莉和朋友共有x人，

若选择包厢计费方案需付：900×6+99x元，

若选择人数计费方案需付：540×x+（6﹣3）×80×x=780x（元），

∴900×6+99x＜780x，

解得：x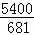＞=7．

∴至少有8人．

故选C

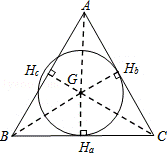
21．如图，G为△ABC的重心．若圆G分别与AC、BC相切，且与AB相交于两点，则关于△ABC三边长的大小关系，下列何者正确？（　）

解析：　　 ∵G为△ABC的重心，

∴△ABG面积=△BCG面积=△ACG面积，

又∵GH_a=GH_b＞GH_c，

∴BC=AC＜AB．

故选D．