
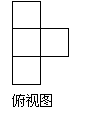 例2、(2008江苏模拟)由大小相同的正方体木块堆成的几何体的三视图如图所示,则该几何体中正方体木块的个数是
.
例2、(2008江苏模拟)由大小相同的正方体木块堆成的几何体的三视图如图所示,则该几何体中正方体木块的个数是
.
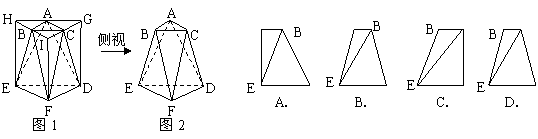

解:在图2的右边放扇墙(心中有墙),可得答案A
点评:本题主要考查三视图中的左视图,要有一定的空间想象能力。
例1、(2008广东)将正三棱柱截去三个角(如图1所示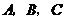 分别是
分别是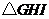 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
二面角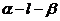 的平面角
的平面角 或
或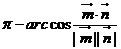 (
( ,
,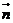 为平面
为平面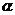 ,
,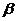 的法向量).
的法向量).
二、考点剖析
考点一:空间几何体的结构、三视图、直观图
【内容解读】了解柱、锥、台、球体及其简单组合体的结构特征,并能运用这些特征描述现实生活中的简单物体的结构。能画出简单空间几何体的三视图,能识别上述三视图所表示的立体模型,会用斜二测画法画出它们的直观图。能用平行投影与中心投影两种方法画出简单空间几何体的三视图与直观图。了解空间几何体的不同表示形式。会画某建筑物的视图与直观图。
空间几何体的结构与视图主要培养观察能力、归纳能力和空间想象能力,能通过观察几何体的模型和实物,总结出柱、锥、台、球等几何体的结构特征;能识别三视图所表示的空间几何体,会用材料制作模型,培养动手能力。
【命题规律】柱、锥、台、球体及其简单组合体的结构特征在旧教材中出现过,而三视图为新增内容,一般情况下,新增内容会重点考查,从2007年、2008年广东、山东、海南的高考题来看,三视图是出题的热点,题型多以选择题、填空题为主,也有出现在解答题里,如2007年广东高考就出现在解答题里,属中等偏易题。
⑤利用法向量求二面角的平面角定理:设 分别是二面角
分别是二面角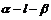 中平面
中平面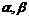 的法向量,则
的法向量,则 所成的角就是所求二面角的平面角或其补角大小(
所成的角就是所求二面角的平面角或其补角大小( 方向相同,则为补角,
方向相同,则为补角, 反方,则为其夹角).
反方,则为其夹角).
④直线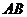 与平面所成角
与平面所成角 (
( 为平面
为平面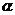 的法向量).
的法向量).
③.点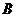 到平面
到平面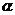 的距离
的距离 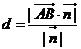 (
(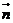 为平面
为平面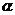 的法向量,
的法向量,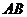 是经过面
是经过面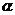 的一条斜线,
的一条斜线,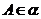 ).
).
②.异面直线间的距离 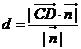 (
( 是两异面直线,其公垂向量为
是两异面直线,其公垂向量为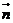 ,
,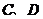 分别是
分别是 上任一点,
上任一点,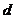 为
为 间的距离).
间的距离).
①利用法向量求点到面的距离定理:如图,设n是平面 的法向量,AB是平面
的法向量,AB是平面 的一条射线,其中
的一条射线,其中 ,则点B到平面
,则点B到平面 的距离为
的距离为 .
.
b.法向量:若向量 所在直线垂直于平面
所在直线垂直于平面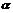 ,则称这个向量垂直于平面
,则称这个向量垂直于平面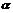 ,记作
,记作 ,如果
,如果 那么向量
那么向量 叫做平面
叫做平面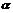 的法向量.
的法向量.
c.用向量的常用方法:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com