
3.平面直角坐标上有点P(-1,-2)和点Q(4,2),取点R(1,m),试问当m为何值时,PR+RQ有最小值.
 试求k的取值范围.
试求k的取值范围.
2.在平面直角坐标系里,点A的坐标是(4,0),点P是第一象限内一次函数y=-x+6的图像上的点,原点是O,如果△OPA的面积为S,P点坐标为(x,y),求S关于x的函数表达式.
1.填空:
(1)已知f(x-1)=19x2+55x-44,则f(x)=_______.
(2)对所有实数x,f(x2+1)=x4+5x2+3,那么对所有实数x,f(x2-1)=_______.
(3)设x与y2成反比例,y与z2成正比例.当x=24时,y=2;当y=18时,z=3,则z=1时,x=_______.
(4)已知y=2x2+mx+5的值恒为正,且m为实数,则m的范围是_______.
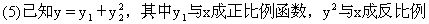
函数,且当x=2,x=3时,y的值都为19,则y的解析式为y=_______.
(6)如果y+m与x+n成正比例,且当x=1时,y=2;当x=-1时,y=1,则y与x间的函数关系式是y=_______.
3.含绝对值的函数
一次函数的图像是一条直线,含有绝对值符号的函数所对应的图像是由若干条线段和射线所组成的折线;二次函数的图像是抛物线,而y=|ax2+bx+c|的图像是将y=ax2+bx+c在x轴下方的图像按x轴为对称轴翻到x轴的上方.对于一些其他的含绝对值符号的函数和方程的图像,需要按区间分段讨论.
例7 作函数y=|3-x|+|x-1|的图像.
解 当x<1时,y=(3-x)+(1-x)=-2x+4;
当1≤x<3时,y=(3-x)+(x-1)=2;当x≥3时,y=(x-3)+(x-1)=2x-4.所以
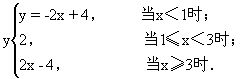
它的图像如图3-3所示.
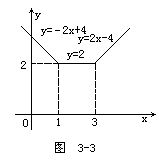
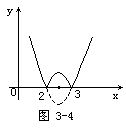
例8 作函数y=|x2-5x+6|的图像.
解 当x≤2或x≥3时,x2-5x+6≥0,于是y=x2-5x+6;当2<x<3时,x2-5x+6<0,于是y=-(x2-5x+6).所以

于是,得图像如图3-4所示.
例9 点(x,y)满足方程
|x-1|+|y+2|=2,
求它的图像所围成区域的面积.
解 当x≥1,y≥-2时,x-1+y+2=2,即
y=-x+1.
当x≥1,x<-2时,x-1-(y+2)=2,即
y=x-5.
当x<1,y≥-2时,-x+1+y+2=2,即
y=x-1.
当x<1,y<-2时,-x+1-(y+2)=2,即
y=-x-3.
于是,所得图像如图3-5所示.
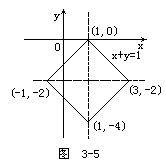
由此可知,|x-1|+|y+2|=2的图像是一个对角线长为4,边长为2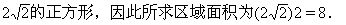
例10 m是什么实数时,方程x2-4|x|+5=m有四个互不相等的实数根?
解法1 将原方程变形为
x2-4|x|+4=m-1.
令y=x2-4|x|+4=m-1,则
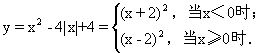
它的图像如图3-6,而y=m-1是一条与x轴平行的直线.原方程有四个互不相等的实根,即直线应与曲线有四个不同的交点.由图像可知,当0<m-1<4,即1<m<5时,直线与曲线有四个不同的交点,所以,当1<m<5时,方程x2-4|x|+5=m有四个互不相等的实数根.
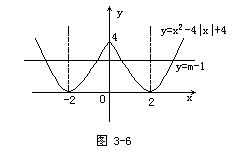
说明 本题是一个方程问题,我们利用图形来研究,这是一种非常重要的思想方法——数形结合法.当然,本题不用图像也是可以解的,下面给出解法,请读者比较一下.
解法2 原方程变形为
(|x|-2)2=m-1,
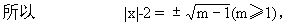
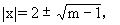
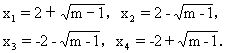
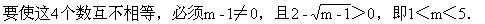
练习五
2.建立函数关系式
例5 直线l1过点A(0,2),B(2,0),直线l2:y=mx+b过点C(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,如图3-1.设此三角形的面积为S,求S关于m的函数解析式,并画出图像.
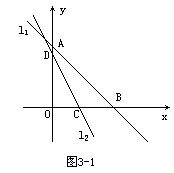
解 因为l2过点C(1,0),所以m+b=0,即b=-m.
设l2与y轴交于点D,则点D的坐标为(0,-m),且0<-m≤2(这是因为点D在线段OA上,且不能与O点重合),即-2≤m<0.
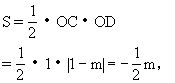
故S的函数解析式为
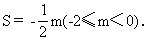
例6 已知矩形的长大于宽的2倍,周长为12.从它的一个顶点作一条射线,将矩形分成一个三角形和一个梯形,且这条射线与矩形一边
 x,试写出梯形面积S关于x的函数关系式.
x,试写出梯形面积S关于x的函数关系式.
解 设矩形ABCD的长BC大于宽AB的2倍.由于周长为12,故长与宽满足4<BC<6,0<AB<2.
由题意,有如下两种情形:
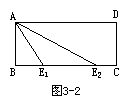
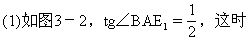
CE1=x,BE1=BC-x,AB=CD=2(BC-x),所以
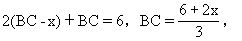
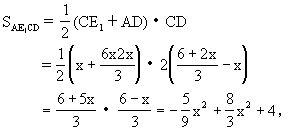
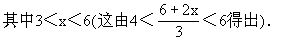
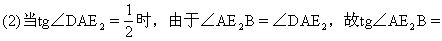
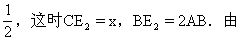
(2AB+x)+AB=6,

所以

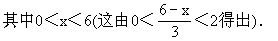
1.求函数值和函数表达式
对于函数y=f(x),若任取x=a(a为一常数),则可求出所对应的y值f(a),此时y的值就称为当x=a时的函数值.我们经常会遇到求函数值与确定函数表达式的问题.
例1 已知f(x-1)=19x2+55x-44,求f(x).
解法1 令y=x-1,则x=y+1,代入原式有
f(y)=19(y+1)2+55(y+1)-44
=19y2+93y+30,
所以 f(x)=19x2+93x+30.
解法2 f(x-1)=19(x-1)2+93(x-1)+30,所以f(x)=19x2+93x+30.

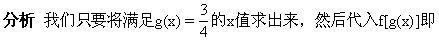 可.
可.
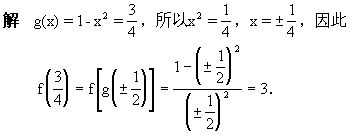
例3 已知函数f(x)=ax5-bx3+x+5,其中a,b为常数.若f(5)=7,求f(-5).
解 由题设
f(-x)=-ax5+bx3-x+5
=-(ax5-bx3+x+5)+10
=-f(x)+10,
所以
f(-5)=-f(5)+10=3.
例4 函数f(x)的定义域是全体实数,并且对任意实数x,y,有f(x+y)=f(xy).若f(19)=99,求f(1999).
解 设f(0)=k,令y=0代入已知条件得
f(x)=f(x+0)=f(x·0)=f(0)=k,
即对任意实数x,恒有f(x)=k.所以
f(x)=f(19)=99,
所以f(1999)=99.
2(巴蜀三模)25.如图,在平面直角坐标系中,抛物线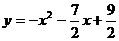 与直线
与直线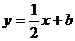 交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合),连接PA、PB。
交于A、B两点,其中点A在x轴上,点P是直线AB上方的抛物线上一动点(不与点A、B重合),连接PA、PB。
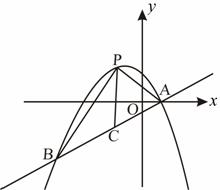 (1)求直线的解析式及A、B两点的坐标;
(1)求直线的解析式及A、B两点的坐标;
(2)过点P作x轴的垂线,交直线AB于点C,当线段PC最大时,求此时点C的坐标及PC的最大值;
(3)当∠PAB=90°时,求此时点P的坐标。
 3(八中二次测试)25、已知二次函数的解析式为
3(八中二次测试)25、已知二次函数的解析式为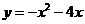 ,该二次函数交x轴于O、B两点,A为抛物线上一点,且横纵坐标相等(原点除外),P为二次函数上一动点,过P作x轴的垂线,垂足为D(a,0)(a>0),并与直线OA交于点C。
,该二次函数交x轴于O、B两点,A为抛物线上一点,且横纵坐标相等(原点除外),P为二次函数上一动点,过P作x轴的垂线,垂足为D(a,0)(a>0),并与直线OA交于点C。
(1)求A、B两点的坐标;
(2)过点P作x轴的平行线与线段OA相交于点E,求△PCE的周长的最大值及此时p点的坐标;
(3)当PC=CO时,求P点的坐标。
25如图,抛物线 2与
2与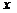 轴交于A、B两点,与
轴交于A、B两点,与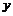 轴交于点C,已知A(–1,0),且tan∠ABC =
轴交于点C,已知A(–1,0),且tan∠ABC = 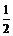 ,作垂直于
,作垂直于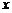 轴的直线
轴的直线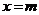 ,与抛物线交于点F,与线段BC交于点E.
,与抛物线交于点F,与线段BC交于点E.
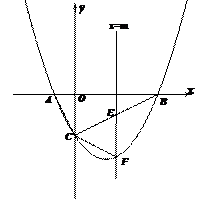 (1)求抛物线的解析式和直线BC的解析式;
(1)求抛物线的解析式和直线BC的解析式;
(2)若△CEF为等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作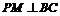 交
交
直线BC于点M,连接PB,若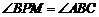 ,求P点的坐标.
,求P点的坐标.
|
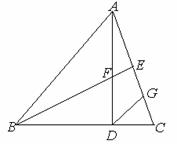
3(西南大学附中六次)24如图,在等腰三角形ABC中,CA = CB,∠ACB = 90°,点D、E是直线BC上两点且CD = BE,过点C作CM⊥AE交AE于点M,交AB于点F,连接DF并延长交AE于点N.
(8)
 若AC = 2,CD = 1,求CM的值;
若AC = 2,CD = 1,求CM的值;
(9) 求证:∠D =∠E.
 4(南开二模)24.如图,在△ABC中,AB=BC,AD⊥BC于D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交于点G.
4(南开二模)24.如图,在△ABC中,AB=BC,AD⊥BC于D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB交于点G.
求证:(1)∠BAD=2∠DAC;(2) .
.
十题25题(1,2问)
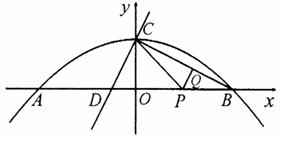 1(南开卷3)25、如图,抛物线
1(南开卷3)25、如图,抛物线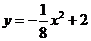 交
交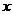 轴于A、B两点(点A在点B的左侧),交
轴于A、B两点(点A在点B的左侧),交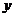 轴于点
轴于点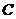 ,连接BC,经过点
,连接BC,经过点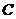 的直线
的直线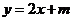 交
交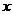 轴于点D。点P为线段DB上的一动点,过点P作
轴于点D。点P为线段DB上的一动点,过点P作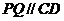 ,交BC于点Q。
,交BC于点Q。
(1)求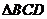 的周长;
的周长;
(2)连接CP,求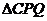 的最大面积,并求出此时
的最大面积,并求出此时
点P的坐标;
(3)设直线PQ与抛物线交于点M,与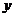 轴交于点
轴交于点
N,连接DM,若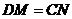 ,求点M的坐标。
,求点M的坐标。
2(八中二次测试) 24、在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E。
24、在△ABC中,∠ACB=90°,AC=BC,过C作CD∥AB交∠ABC的平分线于点D,∠ACB的平分线交BD于点E。
(1)求证:BC=CD;
(2)求证:BC+CE=AB
4(西南大学附中六次)23直辖市之一的重庆,发展的速度是不容置疑的.很多人把重庆作为旅游的首选之地.“不览夜景,未到重庆”.乘游船夜游两江,犹如在星河中畅游,是一个近距离认识重庆的最佳窗口.“两江号”游轮经过核算,每位游客的接待成本为30元.根据市场调查,同一时间段里,票价为40元时,每晚将售出船票600张,而票价每涨1元,就会少售出10张船票.
(6) 若该游轮每晚获得10000元利润,则票价应定为多少元?
(7) 端午节期间,工商管理部门规定游轮船票单价不能低于42元,同时该游轮为提高市场占有率,决定每晚售出船票数量不少于560张,则票价应定为多少元,才能使每晚获得的利润最大?最大利润是多少?
九24题
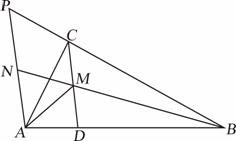 1(巴蜀三模)24.如图,
1(巴蜀三模)24.如图,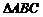 中,
中,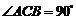 ,D是AB上一点,M是CD中点,且
,D是AB上一点,M是CD中点,且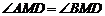 ,
,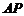 ∥
∥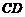 交BC延长线于P点,延长BM交PA于N点,且PN=AN.
交BC延长线于P点,延长BM交PA于N点,且PN=AN.
(1)求证: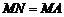 ;
;
(2)求证: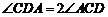 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com