二．填空题：本大题共4小题，每小题5分。

(13)曲线y=x(3lnx+1)在点（1,1）处的切线方程为________

(14)等比数列{a_n}的前n项和为S_n，若S₃+3S₂=0，则公比q=_______

(15)已知向量a,b夹角为45° ，且|a|=1，|2a－b|=，则|b|=　　　

(16)设函数f(x)=的最大值为M，最小值为m，则M+m=____

一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x|x²－x－2<0}，B={x|－1<x<1}，则

（A）AB　 （B）BA　　　　 （C）A=B　　　 （D）A∩B=Æ

（2）复数z＝的共轭复数是　　　　

（A）2+i　 （B）2－i　　　　 （C）－1+i　　　 （D）－1－i

（3）在一组样本数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n）（n≥2，x₁,x₂,…,x_n不全相等）的散点图中，若所有样本点（x_i，y_i）(i=1,2,…,n)都在直线y=x+1上，则这组样本数据的样本相关系数为

（A）－1　 （B）0　　　 （C）　　　 （D）1

（4）设F₁、F₂是椭圆E：＋＝1(a>b>0)的左、右焦点，P为直线x=上一点，△F₁PF₂是底角为30°的等腰三角形，则E的离心率为（　 ）

（A）　 （B）　　　　 （C）　　　 （D）

（5）已知正三角形ABC的顶点A(1,1)，B(1,3)，顶点C在第一象限，若点（x，y）在△ABC内部，则z=－x+y的取值范围是

（A）(1－，2)　　 （B）(0，2)　　 （C）(－1，2)　 （D）(0，1+)

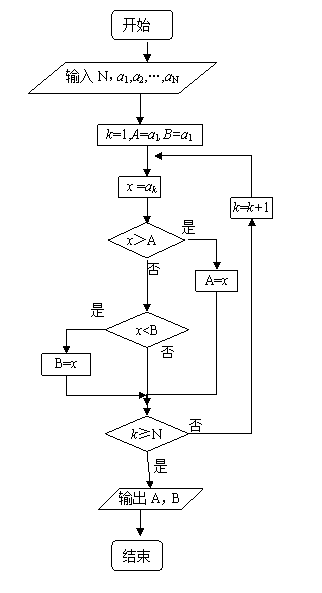
（6）如果执行右边的程序框图，输入正整数N(N≥2)和实数a₁,a₂,…,a_N，输出A,B，则

（A）A+B为a₁,a₂,…,a_N的和

（B）为a₁,a₂,…,a_N的算术平均数

（C）A和B分别是a₁,a₂,…,a_N中最大的数和最小的数

（D）A和B分别是a₁,a₂,…,a_N中最小的数和最大的数

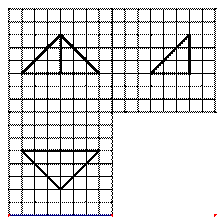
（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为

（A）6　　　　　　　　

（B）9

（C）12

（D）18

(8)平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为

（A）π　 （B）4π　　　　 （C）4π　　　 （D）6π

（9）已知ω>0，0<φ<π，直线x=和x=是函数f(x)=sin(ωx+φ)图像的两条相邻的对称轴，则φ=

（A）　　 　　（B）　　　 （C）　　　 （D）

（10）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y²=16x的准线交于A，B两点，|AB|=4，则C的实轴长为

（A）　　　　 （B）2　　　　 （C）4　　　　　　 （D）8

(11)当0<x≤时，4^x<log_ax，则a的取值范围是

（A）(0，)　　　 （B）(，1)　　　 （C）(1，)　 （D）(，2)

（12）数列{a_n}满足a_n+1＋(－1)ⁿ a_n ＝2n－1，则{a_n}的前60项和为

（A）3690　　　　 （B）3660　　　　 （C）1845　　　　　　 （D）1830

第Ⅱ卷

　本卷包括必考题和选考题两部分。第13题-第21题为必考题，每个试题考生都必须作答，第22-24题为选考题，考生根据要求作答。

24．（本小题满分12分）

已知：如图，在△ABC中， CD⊥AB，垂足为D，BD＝CD＝4cm，AD＝2cm；点P从点A出发，沿AD方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s；当其中一个点停止运动时，另一个点也停止运动．以PQ为底边作等腰三角形PQM，使∠MPQ=∠A，并且△PQM与△ABC分别在AB的两侧，连接PC、QC，设运动时间为t（s）（）． 解答下列问题：

（1）当t为何值时，点D在∠PMQ的平分线上？

（2）设四边形MQCP的面积为y（cm²），求y与t之间的函数关系式；

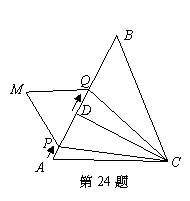（3）是否存在某一时刻t，使S_{四边形MQCP}: S_△ABC = 21：24？若存在，求出此时t的值；若不存在，请说明理由．

(4) 当t为何值时，△PQC是等腰三角形？

解：（1）

（2）

（3）

23．（本小题满分10分）

问题提出：

　　 从A到B共有8个台阶，如果某同学在上台阶时，可以一步1个台阶，也可以一步2个台阶．那么该同学从A走到B共有多少种不同的走法？

问题探究：

为解决上述实际问题，我们先建立如下数学模型：

用若干个边长都为1的正方形（记为矩形）和若干个边长分别为1和2的矩形（记为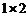矩形），如图①，要拼成一个边长分别为１和n的矩形（记为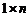矩形），如图②，有多少种不同的拼法？（设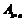表示不同拼法的个数）

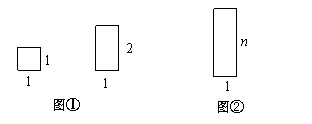
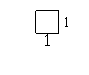
为解决上述数学模型问题，我们采取的策略和方法是：一般问题特殊化．

显然，只有1种拼法，如图③，即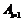=1种．

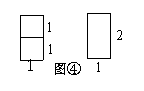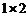探究二：要拼成一个矩形，有多少种不同拼法？

不难看出，有2种拼法，如图④，即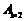=2种．

探究三：要拼成一个矩形，有多少种不同拼法？

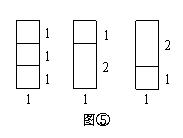拼图方法可分为两类：一类是在图④这2种矩形

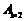上方，各拼上一个矩形，即这类拼法共有=2种；

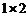另一类是在图③这１种矩形上方拼上一个矩形，

即这类拼法有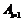=1种，如图⑤．

即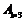=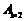+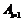= 2+1=3（种）．

探究四：要拼成一个矩形，有多少种不同拼法？

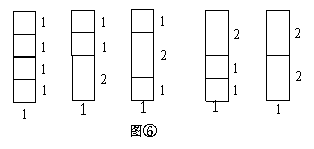拼图方法可分为两类：一类是在图⑤

这3种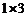矩形上方，各拼上一个

矩形，即这类拼法共有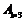=3种；另

一类是在图④这2种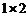矩形上方，

各拼上一个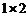矩形，即这类拼法共有

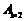=2种，如图⑥．即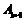=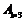+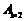=3+2=5（种）．

探究五：要拼成一个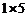矩形，有多少种不同拼法？

仿照上述探究过程进行解答，并求出（不需画图）．

探究六：一般的，要拼成一个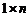矩形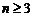（的整数），有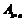＝ 　　 种不同拼法．

（已知，，）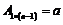

问题解决：把“问题提出”中的实际问题，转化为“问题探究”中的数学模型，并进行解答 ．

22．（本小题满分10分）

某商品每件成品10元，试销阶段调查发现：销售单价是14元时，日销售量是60件，而销售单件每上涨1元，日销售量就减少10件．

(1)　　 写出销售这种商品，每天所得的销售利润y(元)与销售单价x元（元）之间的函数关系式

(2)求销售单价为多少元时，该商品每天的销售利润最大;

(3)据规定，该商品每件的销售利润不得高于每件的成本，且该商品每日的进货成本不超过400元，那么销售该商品每日可获得的最大利润是多少元？

解：（1）

（2）

（3）

21．（本小题满分8分）

已知：如图，在□ABCD中，点E在BC边上，连接A E．O为AE中点，连接BO并延长交AD与F．

　（1）求证：△AOF≌△BOE，

　（2）判断当AE平分∠BAD时，四边形ABEF是什么特殊四边形，并证明你的结论．

　（3）当∠ABC = 　　　　　　　时，四边形AECD为等腰梯形（只写结论，不需证明）．

　证明：（1）

（2）

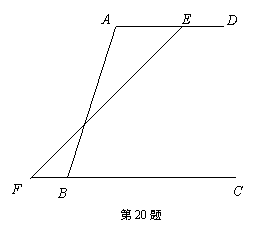
20．（本小题满分8分）

如图，某拦河坝横截面的原设计方案为梯形ABCD，其中AD∥BC，∠ABC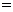72°．为了提高拦河大坝的安全性，现将坝顶宽度水平缩短10m，坝底宽度水平增加4m，使∠EFC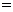45°．

（1）请你计算这个拦河大坝的高度；

（2）请你计算改造后拦河大坝坡面EF的长．（结果保留根号）

（参考数据：sin72°≈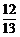 ，cos72°≈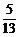，tan72°≈）

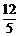解：（1）

（2）

19．（本小题满分6分）

某企业要招聘甲、乙两类技术工人共100人，甲、乙两类技术工人基本月工资分别为800元和1000元．现要求乙类技术工人数不独少于甲类技术工人数的3倍，那么招聘甲类技术工人多少人时，可使每月所付的总工资最少？

18．（本小题满分6分）

我市某书店举行“花香伴书香”抽奖活动，设立了一个可以自由转动的转盘，（如图，转盘被平均分成16份），并规定：顾客每购买300元的书，就可以获得一次转动转盘的机会．如果转盘停止后，指针正好对准梅、兰、菊区域，那么读者就可以分别获得120元、100 元、 60元的购书劵，凭购书劵可以在书城继续购书．如果读者不愿转动转盘，那末可以直接获得25元购书卷．

（1）　　　 写出转动一次转盘获得120元购书卷的概率；

（2）　　　 转动转盘和直接获得购书卷，你认为哪种方式更合算？请说明理由．

2.2 ，2， 2.5，2.5，2.8，2.5，2.2，3，2.8，2.5．

（1）根据以上数据，在图（1）中补全頻数分布直方图

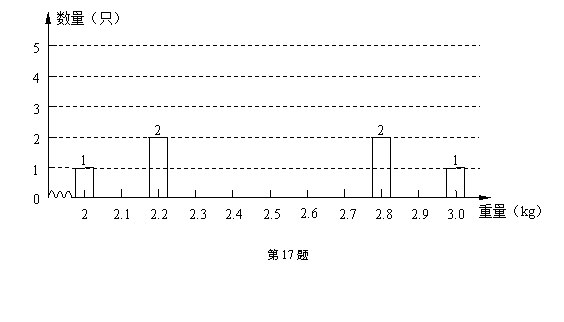
（2）抽取的这10只鸡的质量的众数是　　　　 ，中位数是　　　　 　．

（3）依据这10只鸡的平均质量，估计李辉饲养的1000只鸡总质量是多少？