点评：在课改地区的高考题中，求几何体的表面积与体积的问题经常与三视图的知识结合在一起，综合考查。

因此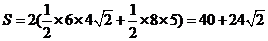  

AB边上的高为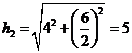  

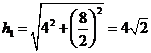    ,  另两个侧面VAB. VCD也是全等的等腰三角形,

(1)

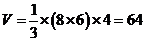
(2) 该四棱锥有两个侧面VAD. VBC是全等的等腰三角形,且BC边上的高为

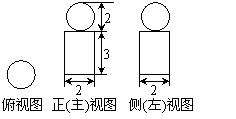
图)是一个底边长为6、高为4的等腰三角形．

  (1)求该几何体的体积V；

  (2)求该几何体的侧面积S

解: 由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V-ABCD。

视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视

例3、（2007广东）已知某几何体的俯视图是如图5所示的矩形，正视图(或称主

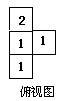解：以俯视图为主，因为主视图左边有两层，表示俯视图中左边最多有两个木块，再看左视图，可得木块数如右图所示，因此这个几何体的正方体木块数的个数为5个。

点评：从三视图到确定几何体，应根据主视图和俯视图情况分析，再结合左视图的情况定出几何体，最后便可得出这个立体体组合的小正方体个数。

考点二：空间几何体的表面积和体积

【内容解读】理解柱、锥、台的侧面积、表面积、体积的计算方法，了解它们的侧面展开图，及其对计算侧面积的作用，会根据条件计算表面积和体积。理解球的表面积和体积的计算方法。

把握平面图形与立体图形间的相互转化方法，并能综合运用立体几何中所学知识解决有关问题。

【命题规律】柱、锥、台、球的表面积和体积以公式为主，按照新课标的要求，体积公式不要求记忆，只要掌握表面积的计算方法和体积的计算方法即可。因此，题目从难度上讲属于中档偏易题。