16．给出下列命题：

①函数y＝cos是奇函数；

②存在实数x，使sinx＋cosx＝2；

③若α，β是第一象限角且α<β，则tanα<tanβ；

④x＝是函数y＝sin的一条对称轴；

⑤函数y＝sin的图像关于点成中心对称．

其中正确命题的序号为__________．

解析　①y＝cos＝－sinx是奇函数．

②因为sinx，cosx不能同时取最大值1，所以不存在实数x使sinx＋cosx＝2成立．

③α＝，β＝，则tanα＝，tanβ＝tan＝tan＝，tanα>tanβ，∴③不成立．

④把x＝代入函数y＝sin，得y＝－1.

∴x＝是函数图像的一条对称轴．

⑤因为y＝sin图像的对称中心在图像上，而不在图像上，所以⑤不成立．

答案　①④

15．已知函数f(x)＝sin(ωx＋φ)(ω>0)的图像如图所示，则ω＝________.

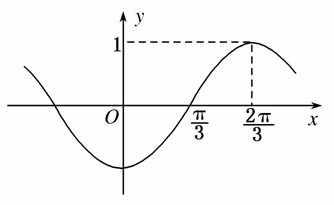
解析　由图知，＝－＝，∴T＝π.

又T＝＝π，∴ω＝.

答案　

14．设α是第三象限的角，tanα＝，则cosα＝________.

解析　借助直角三角形，易知cosα＝－.

答案　－

二、填空题

13．若sinθ＝－，tanθ>0，则cosθ＝________.

解析　由sinθ＝－，tanθ>0知，cosθ<0.

∴cosθ＝－ ＝－ ＝－.

答案　－

12．函数f(x)＝3sin的图像为C，

①图像C关于直线x＝π对称；

②函数f(x)在区间内是增函数；

③由y＝3sin2x的图像向右平移个单位长度可以得到图像C，其中正确命题的个数是(　)

A．0　 B．1　 C．2　 D．3

解析　①把x＝π代入f(x)知，

f＝3sin＝3sin＝－3.

∴x＝π是函数f(x)的对称轴，∴①正确．

②由2kπ－≤2x－≤2kπ＋，得增区间为

(k∈Z)．令k＝0得增区间，∴②正确．

③依题意知y＝3sin2＝3sin，

∴③不正确．应选C.

答案　C

11．已知A为锐角，lg(1＋cosA)＝m，lg＝n，则lgsinA的值是(　)

A．m＋　 　　　　　　　　　　　　　　　　　 B．m－n

C.　 　　　　　　　　　　　　　　　　　 D.(m－n)

解析　∵m－n＝lg(1＋cosA)－lg

＝lg(1＋cosA)＋lg(1－cosA)

＝lg(1＋cosA)(1－cosA)＝lgsin²A＝2lgsinA，

∴lgsinA＝(m－n)，故选D.

答案　D

10．(2011·陕西)函数f(x)＝－cosx在(0，＋∞)内(　)

A．没有零点　 　　　　　　　　　　　　　　 B．有且仅有一个零点

C．有且仅有两个零点　 　　　　　　　 D．有无穷多个零点

解析　在同一坐标系里分别作出y＝和y＝cosx的图像易知，f(x)＝0有且仅有一个零点．

答案　B

9．函数f(x)＝的奇偶性是(　)

A．奇函数

B．偶函数

C．既是奇函数又是偶函数

D．既不是奇函数也不是偶函数

解析　要使f(x)有意义，必须使即

x≠kπ＋，且x≠(2k＋1)π(k∈Z)，

∴函数f(x)的定义域关于原点对称．

又∵f(－x)＝＝－＝－f(x)，

∴f(x)＝是奇函数．

答案　A

8．若tanθ＝2，则的值为(　)

A．0 　　B．1 　　C.　 　　D.

解析　∵tanθ＝2，∴＝＝＝.

答案　C

7．将函数y＝sinx的图像向左平移φ(0≤φ<2π)个单位长度后，得到y＝sin的图像，则φ＝(　)

A. 　　B. 　　C. 　　D.

解析　当φ＝时，则y＝sin

＝sin＝sin.

答案　D