
4、已知R是实数集,M={x 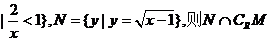 =
=
A.(1,2) B.[0,2] C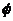 D.[1,2]
D.[1,2]
3、下列有关命题的说法正确的是
A.命题“若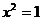 ,则x=l”的否命题为:“若x2 =1,则x≠1”‘
,则x=l”的否命题为:“若x2 =1,则x≠1”‘
B.命题“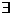 x∈R,使得
x∈R,使得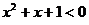 ”的否定是:“
”的否定是:“ x∈R,均有
x∈R,均有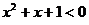 ”;
”;
C.在△ABC中,“A>B”是“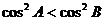 ”的充要条件
”的充要条件
D.“x≠2或y≠1”是“x+y≠3” 的既不充分也不必要条
的既不充分也不必要条 件
件
2、已知集合 ,若
,若 ,则实数
,则实数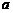 的取值范围是
的取值范围是
A.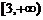 B.
B.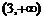 C.
C.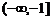 D.
D.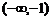
一、选择题
1.下列说法错误的是( )
A.如果命题“¬p”与命题“p∨ q”都是真命题,那么命题q一定是真命题
q”都是真命题,那么命题q一定是真命题
B.命题 “若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
C.若命题p:∃x0∈R,x02+2x0-3<0,则¬p:∀x∈R,x2+2x-3≥0
D.“sin θ=”是“θ=30°”的充分不必要条件
22.(12分)已知函数f(x)=x2+2xtanθ-1,x∈[-1,],其中θ∈.
(1)当θ=-时,求函数的最大值和最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,]上是单调函数(在指定区间为增函数或减函数称为该区间上的单调函数).
解 (1)当θ=-时,
f(x)=x2-x-1=2-.
∵x∈[-1,],
∴当x=时,f(x)的最小值为-,
当x=-1时,f(x)的最大值为.
(2)f(x)=(x+tanθ)2-1-tan2θ是关于x的二次函数.它的图像的对称轴为x=-tanθ.
∵y=f(x)在区间[-1,]上是单调函数,
∴-tanθ≤-1,或-tanθ≥,即tanθ≥1,或tanθ≤-.
∵θ∈,
∴θ的取值范围是∪.
21.(12分)已知cos=cos,
sin=-sin,且0<α<π,
0<β<π,求α,β的值.
解 cos=cos,即sinα=sinβ①
sin=-sin,即cosα=cosβ②
①2+②2得
2=sin2α+3cos2α.
又sin2α+cos2α=1,
∴cos2α=.∴cosα=±.
又∵α∈(0,π),∴α=,或α=π.
(1)当α=时,cosα=,cosβ=cosα=,
又β∈(0,π),∴β=.
(2)当α=时,cosα=-,
cosβ=cosα=-,
又β∈(0,π),∴β=.
综上,α=,β=,或α=,β=.
20.(12分)已知函数y=Asin(ωx+φ)(A>0,ω>0)的图像过点P,图像与P点最近的一个最高点坐标为.
(1)求函数解析式;
(2)求函数的最大值,并写出相应的x的值;
(3)求使y≤0时,x的取值范围.
解 (1)由题意知=-=,∴T=π.
∴ω==2,由ω·+φ=0,得φ=-,又A=5,
∴y=5sin.
(2)函数的最大值为5,此时2x-=2kπ+(k∈Z).∴x=kπ+(k∈Z).
(3)∵5sin≤0,
∴2kπ-π≤2x-≤2kπ(k∈Z).
∴kπ-≤x≤kπ+(k∈Z).
19.(12分)已知f(x)=sin+,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)函数f(x)的图像可以由函数y=sin2x(x∈R)的图像经过怎样变换得到?
解 (1)T==π.
(2)由2kπ+≤2x+≤2kπ+,k∈Z,
得kπ+≤x≤kπ+,k∈Z.
所以所求的单调减区间为(k∈Z).
(3)把y=sin2x的图像上所有点向左平移个单位,再向上平移个单位,即得函数f(x)=sin+的图像.
18.(12分)在△ABC中,sinA+cosA=,求tanA的值.
解 ∵sinA+cosA=,①
两边平方,得2sinAcosA=-,
从而知cosA<0,∴∠A∈.
∴sinA-cosA=
= =.②
由①②,得sinA=,cosA=,
∴tanA==-2-.
三、解答题
17.(10分)已知方程sin(α-3π)=2cos(α-4π),求的值.
解 ∵sin(α-3π)=2cos(α-4π),
∴-sin(3π-α)=2cos(4π-α).
∴-sin(π-α)=2cos(-α).
∴sinα=-2cosα.
可知cosα≠0.
∴原式=
===-.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com