
解:依题意,可得EH∥BD,FG∥BD,故EH∥FG,由公理2可知,E、F、G、H共面,因为EH=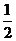 BD,
BD,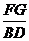 =
=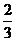 ,故EH≠FG,所以,EFGH是梯形,EF与GH必相交,设交点为M,因为点M在EF上,故点M在平面ACB上,同理,点M在平面ACD上,即点M是平面ACB与平面ACD的交点,而AC是这两个平面的交线,由公理3可知,点M一定在平面ACB与平面ACD的交线AC上。
,故EH≠FG,所以,EFGH是梯形,EF与GH必相交,设交点为M,因为点M在EF上,故点M在平面ACB上,同理,点M在平面ACD上,即点M是平面ACB与平面ACD的交点,而AC是这两个平面的交线,由公理3可知,点M一定在平面ACB与平面ACD的交线AC上。
选(D)。
点评:本题主要考查公理2和公理3的应用,证明共线问题。利用四个公理来证明共点、共线的问题是立体几何中的一个难点。
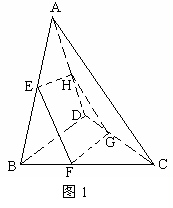 例6、如图1,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且
例6、如图1,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且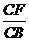 =
= =
=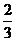 ,则( )
,则( )
(A)EF与GH互相平行
(B)EF与GH异面
(C)EF与GH的交点M可能在直线AC上,也可能不在直线AC上
(D)EF与GH的交点M一定在直线AC上
所以根据球的体积公式知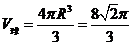 ,故B为正确答案.
,故B为正确答案.
点评:本题考查球的一些相关概念,球的体积公式的运用。
考点三:点、线、面的位置关系
【内容解读】理解空间中点、线、面的位置关系,了解四个公理及其推论;空间两直线的三种位置关系及其判定;异面直线的定义及其所成角的求法。
通过大量图形的观察、实验,实现平面图形到立体图形的飞跃,培养空间想象能力。会用平面的基本性质证明共点、共线、共面的问题。
【命题规律】主要考查平面的基本性质、空间两条直线的位置关系,多以选择题、填空题为主,难度不大。
解:截面面积为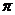
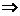 截面圆半径为1,又与球心距离为
截面圆半径为1,又与球心距离为
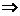 球的半径是
球的半径是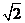 ,
,
A. 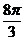 B.
B.
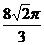 C.
C.
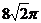 D.
D.
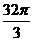
例5、(湖北卷3)用与球心距离为 的平面去截球,所得的截面面积为
的平面去截球,所得的截面面积为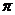 ,则球的体积为( )
,则球的体积为( )
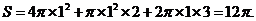 ,故选D。
,故选D。
点评:本小题主要考查三视图与几何体的表面积。既要能识别简单几何体的结构特征,又要掌握基本几何体的表面积的计算方法。
C. D.
D.
解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的简单几何体,
其表面及为:
A. B.
B.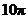
例4、(2008山东)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com