五、解答题

23． 解：（1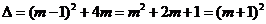），……………………………1分

由知必有，故.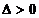

方程①总有两个不相等的实数根. 　……………………………………………2分

（2）令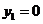，依题意可解得，.

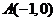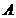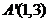∵平移后，点落在点处，

∴平移方式是将点向右平移2个单位，再向上平移3个单位得到.

∴点按相同的方式平移后，点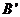为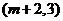.　 ……………………3分

则依题意有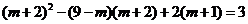. …………………………4分

解得，（舍负）.

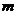的值为3. ………………………………………………………………………5分

（3）.　 ………………………………………………………………………7分

22． 解：（1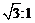）；　　 …………………………………………………………………1分

……………………………………………………………2分

（2）

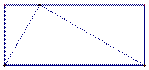
…………………4分

最大三角形的斜边长分别是,．………………………………………………………5分

21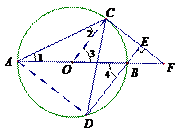． 证明：（1）连接.

∵,

∴.

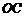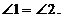又∵

∴

又∵，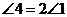

∴ ……………………1分

∴OC∥DB.

∵CE⊥DB，

∴.

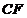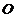又∵为⊙的半径，

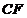∴为⊙O的切线． ………………………………………………………2分

（2）连结.

在Rt△BEF中，∠BEF=90°, BF=5, ，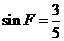

∴. ……………………………………………………………………3分

∵OC∥BE,

∴∽.　

∴

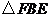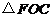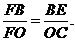
设⊙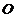的半径为r,

∴

∴.　 ……………………………………………………………………4分

∵AB为⊙O直径，

∴.

∴.

∵,

∴.

∴

∴

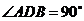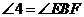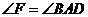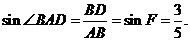
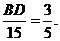
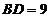∴．……………………………………………………………………5分

20． 解：（1）二；……………………………………………………………………………1分

（2）

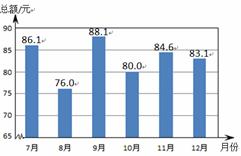
……………………………………3分

（3）三；77. ………………………………………………………………………5分

四、解答题

19．（1）证明：∵点D、E分别是边BC、AC的中点，

∴DE∥AB. ……………………………………………………………………1分

∵AF∥BC,

∴四边形ABDF是平行四边形. ………………………………………………2分

（2）解：过点F作FG⊥AC于G点.

∵BC=4，点D是边BC的中点，

∴BD=2.

由（1）可知四边形ABDF是平行四边形，

∴AF=BD=2.

∵∠CAF=45°，

∴AG=GF=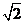. …………………………………………………………………3分

在Rt△FGC中，∠FGC=90°, GF=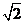，CF=，

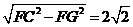∴GC=. …………………………………………………4分

∴AC=AG+GC=.

　……………………………………5分

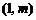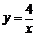18．解：（1）A在的图象上，

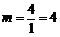∴． …………………………………………………………………………1分

∴A点的坐标为.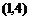

∵A点在一次函数的图象上，

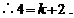
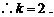
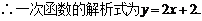　 …………………………………………………2分

令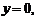即，解得．

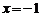点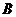的坐标为（-1,0）． ………………………………………………………3分

（2）点P的坐标为（2，2）；点C的坐标为（3，0）. 　………………………………5分

17. 解：设这份快餐含有x克的蛋白质. ……………………………………………………1分

　　　 　根据题意可得: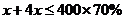，……………………………………………3分

　　　 　解不等式，得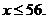　　 …………………………………………………………4分

　　　 　答：这份快餐最多含有56克的蛋白质.　 …………………………………………5分

16. 解：∵

　………………………………………………………………………1分

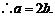　 ……………………………………………………………………………2分

∵，

∴

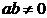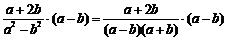
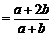　　　　　　　 　　………………………………………………………3分

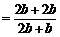　 ………………………………………………………4分

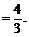　 ……………………………………………………………5分

15.

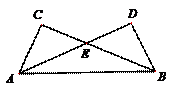证明：在△CAE和△DBE中，

∴△CAE≌△DBE．……………………………………………………………………3分

∴CE=DE． ……………………………………………………………………………4分

∵EA= EB,

∴CE+EB=DE+EA．即BC=AD.　 ……………………………………………………5分

14. _{[来源:ZXXK]}

解：由①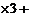②得, .

解得, 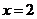.　　 …………………………………………………………………………2分

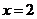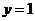把代入①得， .　 ……………………………………………………………4分

∴原方程组的解为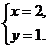 ……….……………………………………………………5分