
8.若2m-4与3m-1是同一个数的平方根,则m的值是( )
A.-3 B.1 C.-3或1 D.-1
7. 若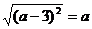 -3,则
-3,则 的取值范围是( ).
的取值范围是( ).
A.  >3 B.
>3 B.  ≥3 C.
≥3 C.  <3 D.
<3 D.  ≤3
≤3
6. 若a、b为实数,且满足│a-2│+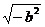 =0,则b-a的值为( )
=0,则b-a的值为( )
A.2 B.0 C.-2 D.以上都不对
5. 下列说法中,不正确的是( ).
A 3是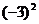 的算术平方根 B±3是
的算术平方根 B±3是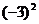 的平方根
的平方根
C -3是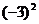 的算术平方根 D.-3是
的算术平方根 D.-3是 的立方根
的立方根
4. 若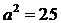 ,
,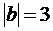 ,则
,则 ( )
( )
A. 8
B.±8 C.±2 D.±8或±2
8
B.±8 C.±2 D.±8或±2
3. 已知下列结论:①在数轴上只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( ).
A.①② B.②③ C.③④ D.②③④
2. 在-1.414, ,π,3.14,2+
,π,3.14,2+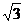 ,3.212212221…,3.14这些数中,无理数的个数为( ).
,3.212212221…,3.14这些数中,无理数的个数为( ).
A.5 B.2 C.3 D.4
一.选择题
1.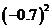 的平方根是( )
的平方根是( )
A.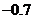 B.
B.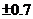 C.
C.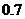 D.
D.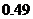
25. 解:
(1)①P2,P3; ……………………………………………………………………2分
②P(-4,6)或P(4,-2). …………………………………………………4分
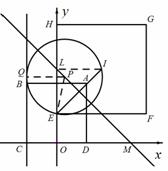
(2)①解:
∵⊙P同时为正方形ABCD与正方形EFGH的“等距圆”,
∴⊙P同时过正方形ABCD的对称中心E和正方形EFGH的对称中心I.
∴点P在线段EI的中垂线上.
∵A(2,4),正方形ABCD的边CD在x轴上;F(6,2),正方形EFGH的边HE在y轴上,
∴E(0,2),I(3,5)
∴∠I EH=45°,
设线段EI的中垂线与y轴交于点L,与x轴交于点M,
∴△LIE为等腰直角三角形,LI⊥y轴,
 ∴L(0,5),
∴L(0,5),
∴△LOM为等腰直角三角形,LO=OM
∴M(5,0),
∴P在直线y=-x+5上,
 ∴设P(p,-p+5)
∴设P(p,-p+5)
过P作PQ⊥直线BC于 Q,连结PE,
Q,连结PE,
∵⊙P与BC所在直线相切,
∴PE =PQ,
=PQ,
∴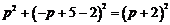 ,
,
解得: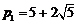 ,
, ,
,
∴. . .……………………………………5分
. .……………………………………5分
∵⊙P过点E,且E点 在y轴上,
在y轴上,
∴⊙P在y轴上截得的弦长为 .…6分
.…6分
②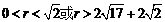 .…………………………………………………8分
.…………………………………………………8分
注:其他解法请参照给分.
24. 解:
解:
(1)
………………………………………………… 2分
2分
(2)连接BF.
∵将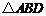 沿射线
沿射线 方向平移,得到
方向平移,得到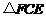 ,
,
∴AD∥EF, AD=EF;AB∥FC, AB=FC.
∵∠ABC=90°,
 ∴四边形ABCF为矩形.
∴四边形ABCF为矩形.
∴AC=BF. ……………………………………3分
∵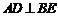 ,
,
∴ .
…………………………………4分
.
…………………………………4分
∵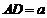 ,
,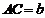 ,
,
∴ ,
,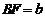 .
.
∴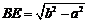 .
………………………………………………………………5分
.
………………………………………………………………5分
(3)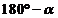 ;
; 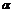 .
………………
.
……………… ………………………
……………………… ……………………7分
……………………7分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com