
例10、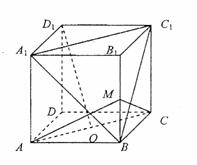 (2008广东五校联考)正方体ABCD―A1B
(2008广东五校联考)正方体ABCD―A1B
(1)D1O//平面A1BC1;
(2)D1O⊥平面MAC.
考点五:直线与平面、平面与平面垂直的判定与性质
【内容解读】掌握直线与平面垂直、平面与平面垂直的判定与性质定理,能用判定定理证明线线垂直、线面垂直、面面垂直,会用性质定理解决线面垂直、面面垂直的问题。
通过线面垂直、面面垂直的证明,培养学生空间观念及及观察、操作、实验、探索、合情推理的能力。
【命题规律】主要考查线线、面面垂直的判定与性质,多以选择题和解答题形式出现,解答题中多以证明线线垂直、线面垂直、面面垂直为主,属中档题。
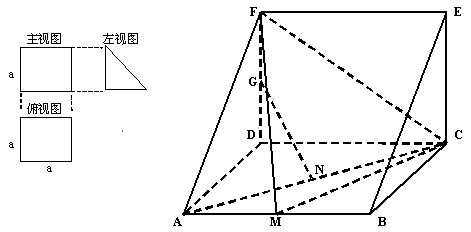
(1)求证: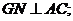
(2)当FG=GD时,在棱AD上确定一点P,使得GP//平面FMC,并给出证明.
例9、(2008江苏模拟)一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
(Ⅰ)证明:直线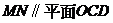
 ;
;
(Ⅱ)求异面直线AB与MD所成角的大小;
(Ⅲ)求点B到平面OCD的距离。
例8、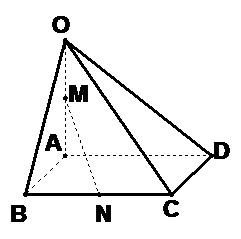 (2008安徽)如图,在四棱锥
(2008安徽)如图,在四棱锥 中,底面
中,底面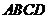 四边长为1的菱形,
四边长为1的菱形,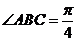 ,
,
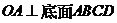 ,
,
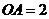 ,
,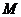 为
为 的中点,
的中点,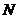 为
为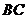 的中点
的中点
于是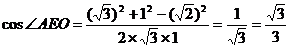 ,故选C。
,故选C。
点评:求异面直线所成的角,一般是平移异面直线中的一条与另一条相交构成三角形,再用三角函数的方法或正、余弦定理求解。
考点四:直线与平面、平面与平面平行的判定与性质
【内容解读】掌握直线与平面平行、平面与平面平行的判定与性质定理,能用判定定理证明线面平行、面面平行,会用性质定理解决线面平行、面面平行的问题。
通过线面平行、面面平行的证明,培养学生空间观念及及观察、操作、实验、探索、合情推理的能力。
【命题规律】主要考查线线、面面平行的判定与性质,多以选择题和解答题形式出现,解答题中多以证明线面平行、面面平行为主,属中档题。
解:连接AC、BD交于O,连接OE,因OE∥SD.所以∠AEO为异面直线SD与AE所成的角。设侧棱长与底面边长都等于2,则在ㄓAEO中,OE=1,AO=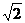 ,AE=
,AE=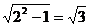 ,
,
A.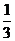 B.
B. C.
C. D.
D.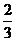
例7、(2008全国二10)已知正四棱锥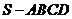 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等,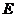 是
是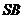 的中点,则
的中点,则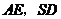 所成的角的余弦值为(
)
所成的角的余弦值为(
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com