
二、填空题
9.
分解因式: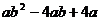 =_________________
=_________________
8.
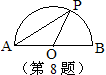
如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为 ,△APO的面积为
,△APO的面积为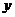 ,则下列图象中,能表示
,则下列图象中,能表示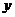 与
与 的函数关系的图象大致是
的函数关系的图象大致是
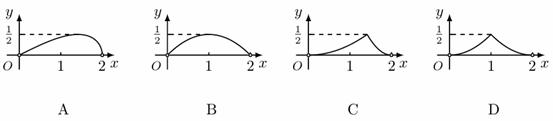
7. 某中学随机地调查了50名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
|
时间(小时) |
5 |
6 |
7 |
8 |
|
人数 |
10 |
15 |
20 |
5 |
则这50名学生这一周在校的平均体育锻炼时间是
 A. 6.2小时 B.
6.4小时
C. 6.5小时
D. 7小时
A. 6.2小时 B.
6.4小时
C. 6.5小时
D. 7小时
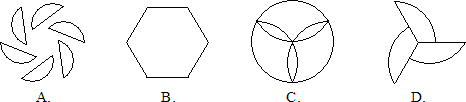
6. 下列图形中,是中心对称图形但不是轴对称图形的是
5.
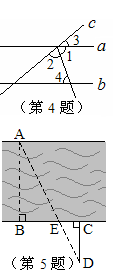
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C ,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于
,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于
A. 60m B. 40m
C. 30m D. 20m
4. 如图,直线
如图,直线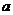 ,
,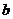 被直线
被直线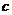 所截,
所截,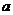 ∥
∥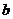 ,∠1=∠2,若∠3=40°,则∠4等于
,∠1=∠2,若∠3=40°,则∠4等于
A. 40° B. 50°
C. 70° D. 80°
3. 在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率为
A. 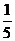 B.
B.
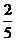 C.
C.
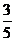 D.
D.
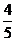
2.
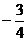 的倒数是
的倒数是
A. 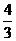 B.
B.
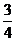 C.
C.
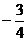 D.
D.
一、选择题
下面各题均有四个选项,其中只有一个是符合题意的。
1.
在《关于促进城市南部地区加快发展第二阶段行动计划(2013-2015)》中,北 京市提出了总计约3 960亿元的投资计划。将3 960用科学计数法表示应为
京市提出了总计约3 960亿元的投资计划。将3 960用科学计数法表示应为
A. 39.6×102 B. 3.96×103 C. 3.96×104 D. 3.96×104
四、用重要不等式证明不等式
应用重要不等式证明不等式的规律和变形的技巧较多,应灵活掌握. 同时要注意不同的题型结构,用不同的方法技巧应对。下面举例说明
例14 已知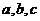 都是正数,求证:
都是正数,求证: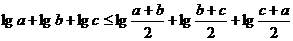 .
.
证法1 ∵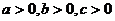 ,∴
,∴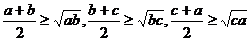 ,
,
三式相乘得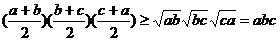 ,两边取常用对数得
,两边取常用对数得
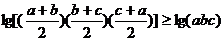 ,即
,即 .
.
证法2 ∵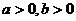 ,∴
,∴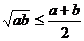 ,两边取常用对数得
,两边取常用对数得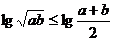 ,即
,即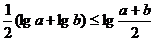 ,同理得
,同理得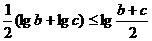 ,
,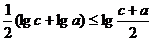 .
.
三式相加得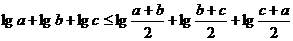 .
.
点评:因为待证的不等式具有对称轮换的结构特征,所以一般要连续使用重要不等式;之后再变形的方法技巧有:两边取对数,各式相加,各式相乘等.
例15 已知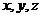 都是正数,且
都是正数,且 ,求证:
,求证: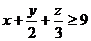 .
.
证明 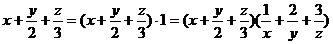
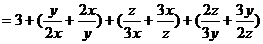
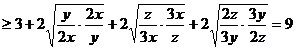 .
.
故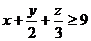 . (当且仅当
. (当且仅当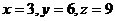 时取等号)
时取等号)
点评:先变形后再用重要不等式,其变形的技巧有:拆并项,凑配项,添零乘壹,平方开方等;若待证不等式的一边是常数,则变形的目的是为了使用重要不等式时,其积(或和)是一个定值,并且等号取得到.
例16 设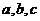 为不全相等的正数,求证:
为不全相等的正数,求证: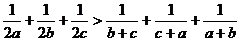 .
.
证明 ∵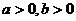 ,∴
,∴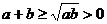 ,从而
,从而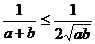 ;
;
又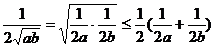 ,∴
,∴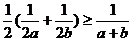 .
.
同理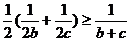 ,
, .
.
∵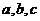 不全相等,∴三个不等式的等号不能同时取到,故三式相加得
不全相等,∴三个不等式的等号不能同时取到,故三式相加得
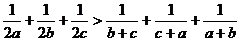 .
.
点评:用了重要不等式后,其重要不等式本身也可以变形,变形的技巧有:取倒数,两边同时加上一个数(或式),两边同时除以一个数(或式)等;变形的目的是为了再次使用重要不等式,从而由不等式的传递性达到目的..
例17 已知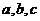 都是正数,且
都是正数,且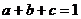 ,求证:
,求证: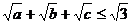 .
.
证法1 ∵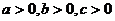 ,则
,则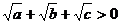 ,
,
∴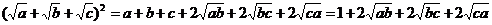 .
.
又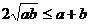 ,
, ,
,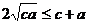 ,
,
∴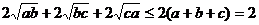 ,
,
故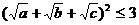 ,即
,即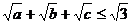 .
.
证法2 ∵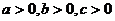 ,
,
∴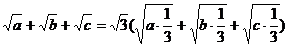
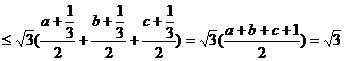 .
.
故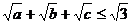 .
.
点评:,例15是先用条件再用重要不等式,而例4是先用重要不等式再用条件. 仔细体会,才有收获,才能融会贯通.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com