
3.物体做匀速圆周运动时,如果向心力突然消失,则下列说法正确的是( )
A.物体将继续在原来的圆周上运动
B.物体将沿着圆周的切线方向飞出去
C.物体将沿着切线和圆周之间的某一条曲线向远离圆心的方向运动
D.以上说法均不对
解析:选B 做匀速圆周运动的物体,任一位置的速度方向均沿该点圆周的切线方向。当向心力突然消失时,物体由于具有惯性,将沿圆周的切线方向飞出去,故B项正确。

 |
传动装置问题 |
 [命题分析] 传动装置问题考查了圆周运动各物理量的关系,在高考中常被考查到,考查的题型一般为选择题。
[命题分析] 传动装置问题考查了圆周运动各物理量的关系,在高考中常被考查到,考查的题型一般为选择题。
[例1] 如图4-3-4所示,一种向自行车车灯供电的小发电机的上端有一半径r0=1.0 cm的摩擦小轮,小轮与自行车车轮的边沿接触。当车轮转动时,因摩擦而带动小轮转动,从而为发电机提供动力。自行车车轮的半径R1=35 cm,小齿轮的半径R2=4.0 cm,大齿轮的半径R3=10.0 cm。求大齿轮的转速n1和摩擦小轮的转速n2之比。(假定摩擦小轮与自行车车轮之间无相对滑动)
cm。求大齿轮的转速n1和摩擦小轮的转速n2之比。(假定摩擦小轮与自行车车轮之间无相对滑动)
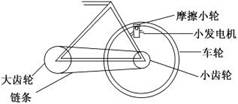
图4-3-4
[解析] 大小齿轮间、摩擦小轮和车轮之间和皮带传动原理相同,两轮边沿各点的线速度大小相等,由v=2πnr可知转速n和半径r成反比;小齿轮和车轮同轴转动,两轮上各点的转速相同。大齿轮与小齿轮转速之间的关系为:n1∶n小=R2∶R3。车轮与小齿轮之间的转速关系为:n车=n小。车轮与摩擦小轮之间的关系为:n车∶n2=r0∶R1。由以上各式可解出大齿轮和摩擦小轮之间的转速之比为:n1∶n2=2∶175。
[答案] 2∶175
[变式训练]
2.近心运动
当提供向心力的合力大于做圆周运动所需向心力时,即F>mω2r,物体将逐渐靠近圆心,做近心运动。

(1)物体做离心运动并非物体受到所谓离心力作用,而是物体惯性的表现。
(2)物体做离心运动时,并非沿半径方向飞出,而是运动半径越来越大或沿切线方向飞出。
1.离心运动
(1)定义:做圆周运动的物体,在所受合力突然消失或不足以提供圆周运动所需向心力的情况下,所做的逐渐远离圆心的运动。
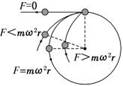
图4-3-3
(2)本质:做圆周运动的物体,由于本身的惯性,总有沿着圆周切线方向飞出去的倾向。
(3)受力特点:
①当F=mω2r时,物体做匀速圆周 运动;
运动;
②当F=0时,物体沿切线方向飞出;
③当F<mω2r时,物体逐渐远离圆心,做离心运动。
2.如图4-3-2所示,某物体沿光滑圆弧轨道由最高点滑到最低点过程中,物体的速率逐渐增大,则( )

图4-3-2
A.物体的合外力为零
B .物体的合力大小不变,方向始终指向圆心O
.物体的合力大小不变,方向始终指向圆心O
C.物体的合外力就是向心力
D.物体的合 力方向始终与其运动方向不垂直(最低点除外)
力方向始终与其运动方向不垂直(最低点除外)
解析:选D 物体做加速曲线运动,合力不为零,A错;物体做速度大小变化的圆周运动,合力不指向圆心,合力沿半径方向的分力等于向心力,合力沿切线方向的分力使物体速度变大,即除在最低点外,物体的速度方向与合外力的方向夹角为锐角,合力与速度不垂直,B、C错,D对。
 |
离心运动和近心运动 |
2.非匀速圆周运动
(1)定义:线速度大小、方向均发生变化的圆周运动。
(2)合力的作用:
①合力沿速度方向的分量Ft产生切向加速度,
Ft=mat,它只改变速度的大小。
②合力沿半径方向的分量Fn产生向心加速度,
Fn=man,它只改变速度的方向。

竖直面内圆周运动问题分析
物体在竖直面内做的圆周运动是一种典型的变速曲线运动,该类运动常有临界问题,并有“最大”、“最小”、“刚好 ”等词语,常有两种模型——轻绳模型和轻杆模型,分析比较如下:
”等词语,常有两种模型——轻绳模型和轻杆模型,分析比较如下:
|
|
轻绳模型 |
轻杆模型 |
|
常见类型 |
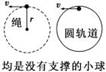 |
 |
|
过最高点的临界条件 |
|
由小球能运动即可,得v临=0 |
|
讨论分析 |
(1)过最高点时,v≥,FN+mg=m,绳、轨道对球产生弹力FN (2)不能过最高点时v<,在到达最高点前小球已经脱离了圆轨道 |
(1)当v=0时,FN=mg,FN为支持力,沿半径背离圆心 (2)当0<v<时,-FN+mg=m,FN背离圆心且随v的增大而减小 (3)当v=时,FN=0 (4)当v>时,FN+mg=m,FN指向圆心并随v的增大而增大 |
1.匀速圆周运动
(1)定义:线速度大小不变的圆周运动。
(2)性质:向心加速度大小不变,方向总是指向圆心的变加速曲线运动。
(3)质点做匀速圆周运动的条件:
合力大小不变,方向始终与速度方向垂直且指向圆心。
1.如图4-3-1所示,甲、乙、丙三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为( )
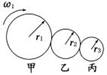
图4-3-1
A. B.
C. D.
解析:选A 本题相当于皮带轮的连接,各个轮边缘的线速度大小相同。即v1=ω1r1=v2=ω2r2=v3=ω3 r3,故A选项正确。
r3,故A选项正确。
 |
匀速圆周运动和非匀速圆周运动 |
2.用动力学方法解决圆周运动中的问题
(1)向心力的来源:向心力是按力的作用效果命名的,可以是重力、弹力、摩擦力等各种力,也可以是几个力的合力或某个力的分力,因此在受力分析中要避免再另外添加一个向心力。
(2)向心力的确定:
①确定圆周运动的轨道所在的平面,确定圆心的位置。
②分析物体的受力情况,找出所有的力,沿半径方向指向圆心的合力就是向心力。
(3)解决圆周运动问题的主要步骤:
①审清题意,确定研究对象;
②分析物体的运动情况,即物体的线速度、角速度、周期、轨道平面、圆心、半径等;
③分析物体的受力情况,画出受力示意图,确定向心力的来源;
④根据牛顿运动定律及向心力公式列方程;
⑤求解、讨论。
1.在传动装置中各物理量的关系
(1)同一转轴的各点角速度ω相 同,而线速度v=ωr与半径r成正比,向心加速度大小an=rω2与半径r成正比。
同,而线速度v=ωr与半径r成正比,向心加速度大小an=rω2与半径r成正比。
(2)当皮带不打滑时,传动皮带、用皮带连接的两轮边缘上各点的线速度大小相等,两皮带轮上各点的角速度、向心加速度关系可根据ω=、an=确定。
23.[解题思路](1)①平衡好小车所受的阻力,小车做匀速运动,打点计时器打出的点间隔基本相等⑥根据牛顿第二定律可知,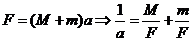 ,
, 与m为一次函数关系,是线性关系。(2)(i)为保证小车所受拉力近似不变,应满足小吊盘和盘中物块的质量之和远小于小车的质量。(ii)由
与m为一次函数关系,是线性关系。(2)(i)为保证小车所受拉力近似不变,应满足小吊盘和盘中物块的质量之和远小于小车的质量。(ii)由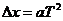 可知,
可知,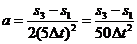 ,由图可读出
,由图可读出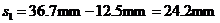 ,
,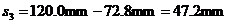 ,换算后代入上式中,得
,换算后代入上式中,得 (iii)设小车质量为M,由牛顿第二定律可得:
(iii)设小车质量为M,由牛顿第二定律可得: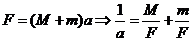 ,结合图象可知,
,结合图象可知,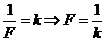 ,
,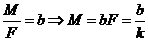
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com