
17、(福建卷)如图(甲)所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复。通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图像如图(乙)所示,则

A.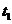 时刻小球动能最大
时刻小球动能最大
B.  时刻小球动能最大
时刻小球动能最大
C.  ~
~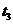 这段时间内,小球的动能先增加后减少
这段时间内,小球的动能先增加后减少
D.  ~
~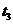 这段时间内,小球增加的动能等于弹簧减少的弹性势能
这段时间内,小球增加的动能等于弹簧减少的弹性势能
[答案]C
[解析]小球在接触弹簧之前做自由落体。碰到弹簧后先做加速度不断减小的加速运动,当加速度为0,即重力等于弹簧弹力时速度达到最大值,而后往下做加速度不断增大的减速K^S*5U运动,与弹簧接触的整个下降过程,小球的动能和重力势能转化为弹簧的弹性势能。上升过程恰好与下降过程互逆。由乙图可知t1时刻开始接触弹簧;t2时刻弹力最大,小球处在最低点,动能最小;t3时刻小球往上运动恰好要离开弹簧;t2-t3这段时间内,小球的先加速后减速,动能先增加后减小,弹簧的弹性势能转化为小球的动能和重力势能。
[命题特点]本题考查牛顿第二定律和传感器的应用,重点在于考查考生对图像的理解。
[启示]图像具有形象快捷的特点,考生应深入理解图像的含义并具备应用能力。
15.(江苏卷)(16分)制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示,加在极板A、B间的电压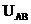 作周期性变化,其正向电压为
作周期性变化,其正向电压为 ,反向电压为
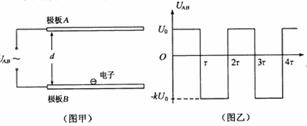
,反向电压为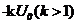 ,电压变化的周期为2r,如图乙所示。在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动。若整个运动过程中,电子未碰到极板A,且不考虑重力作用。
,电压变化的周期为2r,如图乙所示。在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动。若整个运动过程中,电子未碰到极板A,且不考虑重力作用。
(1)若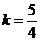 ,电子在0—2r时间内不能到达极板A,求d应满足的条件;
,电子在0—2r时间内不能到达极板A,求d应满足的条件;
(2)若电子在0—2r时间未碰到极板B,求此运动过程中电子速度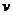 随时间t变化的关系;
随时间t变化的关系;
(3)若电子在第N个周期内的位移为零,求k的值。
解析:
(1)电子在0~T时间内做匀加速运动
加速度的大小
 ①
①
位移 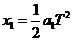 ②
②
在T-2T时间内先做匀减速运动,后反向作匀加速运动
加速度的大小
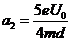 ③
③
初速度的大小  ④
④
匀减速运动阶段的位移
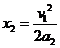 ⑤
⑤
依据题意  >
> 解得
解得 >
>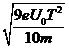 ⑥
⑥
(2)在2nT~(2n+1)T,(n=0,1,2, ……,99)时间内 ⑦
加速度的大小 a′2=
速度增量 △v2=-a′2T ⑧
(a)当0≤t-2nt<T时
电子的运动速度 v=n△v1+n△v2+a1(t-2nT) ⑨
解得 v=[t-(k+1)nT]
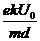 ,(n=0,1,2, ……,99) ⑩
,(n=0,1,2, ……,99) ⑩
(b)当0≤t-(2n+1)T<T时
电子的运动速度 v=(n+1) △v1+n△v2-a′2[t-(2n+1)T] 11
解得v=[(n+1)(k+1)T-kl]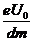 ,(n=0,1,2, ……,99) 12
,(n=0,1,2, ……,99) 12
(3)电子在2(N-1)T~(2N-1)T时间内的位移x2N-1=v2N-2T+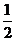 a1T2
a1T2
电子在(2N-1)T~2NT时间内的位移x2N=v2N-1T-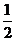 a′2T2
a′2T2
由10式可知 v2N-2=(N-1)(1-k)T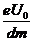
由12式可知 v2N-1=(N-Nk+k)T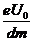
依据题意 x2N-1+ x2N=0
解得
本题考查牛顿运动定律、运动学公式应用和归纳法解题。
难度:难。
32.(上海物理)(14分)如图,宽度L=0.5m的光滑金属框架MNPQ固定板个与水平面内,并处在磁感应强度大小B=0.4T,方向竖直向下的匀强磁场中,框架的电阻非均匀分布,将质量m=0.1kg,电阻可忽略的金属棒ab放置在框架上,并且框架接触良好,以P为坐标原点,PQ方向为x轴正方向建立坐标,金属棒从 处以
处以 的初速度,沿x轴负方向做
的初速度,沿x轴负方向做 的匀减速直线运动,运动中金属棒仅受安培力作用。求:
的匀减速直线运动,运动中金属棒仅受安培力作用。求:
(1)金属棒ab运动0.5m,框架产生的焦耳热Q;
(2)框架中aNPb部分的电阻R随金属棒ab的位置x变化的函数关系;
(3)为求金属棒ab沿x轴负方向运动0.4s过程中通过ab的电量q,某同学解法为:先算出金属棒的运动距离s,以及0.4s时回路内的电阻R,然后代入
q=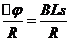
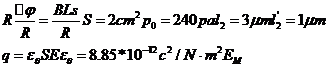 求解。指出该同学解法的错误之处,并用正确的方法解出结果。
求解。指出该同学解法的错误之处,并用正确的方法解出结果。
解析:
(1)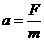 ,
,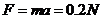
因为运动中金属棒仅受安培力作用,所以F=BIL
又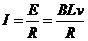 ,所以
,所以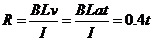
且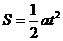 ,得
,得
所以
(2)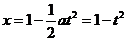 ,得
,得 ,所以
,所以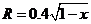 。
。
(3)错误之处:因框架的电阻非均匀分布,所求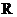 是0.4s时回路内的电阻R,不是平均值。
是0.4s时回路内的电阻R,不是平均值。
正确解法:因电流不变,所以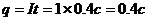 。
。
本题考查电磁感应、电路与牛顿定律、运动学公式的综合应用。难度:难。
11.(上海物理) 将一个物体以某一速度从地面竖直向上抛出,设物体在运动过程中所受空气阻力大小不变,则物体
(A)刚抛出时的速度最大 (B)在最高点的加速度为零
(C)上升时间大于下落时间 (D)上升时的加速度等于下落时的加速度
解析: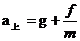 ,
,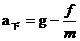 ,所以上升时的加速度大于下落时的加速度,D错误;
,所以上升时的加速度大于下落时的加速度,D错误;
根据 ,上升时间小于下落时间,C错误,B也错误,本题选A。
,上升时间小于下落时间,C错误,B也错误,本题选A。
本题考查牛顿运动定律和运动学公式。难度:中。
17、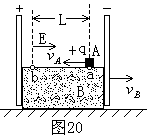 (2009年广东物理)20.如图20所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极板间形成匀强电场E。长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同)。B与极板的总质量mB=1.0kg。带正电的小滑块A质量mA=0.60kg,其受到的电场力大小F=1.2N。假设A所带的电量不影响极板间的电场分布。t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.5m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动。问(g取10m/s2)
(2009年广东物理)20.如图20所示,绝缘长方体B置于水平面上,两端固定一对平行带电极板,极板间形成匀强电场E。长方体B的上表面光滑,下表面与水平面的动摩擦因数μ=0.05(设最大静摩擦力与滑动摩擦力相同)。B与极板的总质量mB=1.0kg。带正电的小滑块A质量mA=0.60kg,其受到的电场力大小F=1.2N。假设A所带的电量不影响极板间的电场分布。t=0时刻,小滑块A从B表面上的a点以相对地面的速度vA=1.5m/s向左运动,同时,B(连同极板)以相对地面的速度vB=0.40m/s向右运动。问(g取10m/s2)
(1)A和B刚开始运动时的加速度大小分别为多少?
(2)若A最远能到达b点,a、b的距离L应为多少?从t=0时刻至A运动到b点时,摩擦力对B做的功为多少?
答案:(1)2m/s2,方向水平向右;2m/s2,方向水平向左
(2)0.62m,-0.072J
[解析](1)A、B刚开始运动时,由牛顿第二定律,得
对于A,只受电场力,有 
得A的加速度大小为 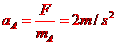 ,方向水平向右
,方向水平向右
对于B及极板,由牛顿第三定律知所受电场力为

由牛顿第二定律得 
而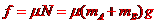
得B的加速度大小为 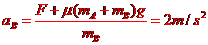 方向水平向左
方向水平向左
(2)A、B开始时都做加速度为 的匀减速直线运动,而
的匀减速直线运动,而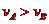 ,故B先减速到0,设从
,故B先减速到0,设从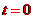 到B速度减为0的时间为
到B速度减为0的时间为 ,则
,则

得 
在 时间内,A的向左运动的位移为
时间内,A的向左运动的位移为

B向右运动的位移为
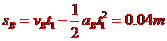
 时,A的速度为
时,A的速度为
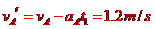
此后A继续向左做加速度为 的匀减速直线运动,而B受到向左的电场力
的匀减速直线运动,而B受到向左的电场力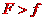 ,故B向左做匀加速运动,设经时间
,故B向左做匀加速运动,设经时间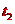 ,A、B速度达到相同的
,A、B速度达到相同的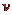 ,则
,则
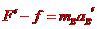 得
得 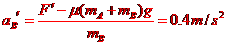

得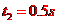
在时间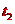 内,A向左的位移为
内,A向左的位移为
B向左的位移为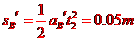
则a、b间距离为
在此过程中摩擦力对B做的功为
2010年高考物理试题分类汇编——牛顿运动定律
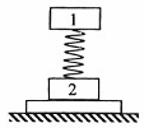 (全国卷1)15.如右图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为
(全国卷1)15.如右图,轻弹簧上端与一质量为m的木块1相连,下端与另一质量为M的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态。现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为 、
、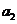 。重力加速度大小为g。则有
。重力加速度大小为g。则有
A. ,
, B.
B.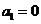 ,
,
C.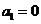 ,
,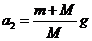 D.
D. ,
,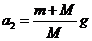
[答案]C
[解析]在抽出木板的瞬时,弹簧对1的支持力和对2的压力并未改变。对1物体受重力和支持力,mg=F,a1=0.
对2物体受重力和压力,根据牛顿第二定律
[命题意图与考点定位]本题属于牛顿第二定律应用的瞬时加速度问题,关键是区分瞬时力与延时力。
16、 (2009年上海物理)22.如图(a),质量m=1kg的物体沿倾角q=37°的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示。求:
(2009年上海物理)22.如图(a),质量m=1kg的物体沿倾角q=37°的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示。求:
(1)物体与斜面间的动摩擦因数m;
(2)比例系数k。(sin370=0.6,cos370=0.8,g=10m/s2)
[解析]ww.ks5u.com(1)对初始时刻:mgsinq-mmgcosq=ma0 ①,由右图读出a0=4m/s2代入①式,
解得:m==0.25;
(2)对末时刻加速度为零:mgsinq-mN-kvcosq=0 ②,又N=mgcosq+kvsinq ③,
由右图得出此时v=5 m/s代入②③式解得:k==0.84kg/s。
15、(2009年海南物理)15.一卡车拖挂一相同质量的车厢,在水平直道上以v0=12m/s的速度匀速行驶,其所受阻力可视为与车重成正比,与速度无关。某时刻,车厢脱落,并以大小为a=2m/s2的加速度减速滑行。在车厢脱落t=3s后,司机才发觉并紧急刹车,刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变,求卡车和车厢都停下后两者之间的距离。
解析:设卡车的质量为M,车所受阻力与车重之比为μ;刹车前卡车牵引力的大小为F,卡车刹车前后加速度的大小分别为a1和a2。重力加速度大小为g。由牛顿第二定律有
匀速行驶
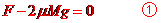
车厢脱落卡车刹车前 
由①②可得:

车厢脱落卡车刹车后 
设车厢脱落后, 内卡车行驶的路程为
内卡车行驶的路程为 ,末速度为
,末速度为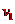 ,根据运动学公式有
,根据运动学公式有
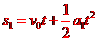 ⑤
⑤
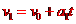 ⑥
⑥
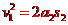 ⑦
⑦
式中, 是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为
是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为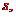 有
有 ⑧
⑧
卡车和车厢都停下来后相距 ⑨
⑨
由①至⑨式得 ⑾
⑾
带入题给数据得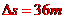 ⑿
⑿
14、(2009年江苏卷)13.航模兴趣小组设计出一架遥控飞行器,其质量m =2㎏,动力系统提供的恒定升力F =28 N。试飞时,飞行器从地面由静止开始竖直上升。设飞行器飞行时所受的阻力大小不变,g取10m/s2。
(1)第一次试飞,飞行器飞行t1 = 8 s 时到达高度H = 64 m。求飞行器所阻力f的大小;
(2)第二次试飞,飞行器飞行t2 = 6 s 时遥控器出现故障,飞行器立即失去升力。求飞行器能达到的最大宽度h;
(3)为了使飞行器不致坠落到地面,求飞行器从开始下落到恢复升力的最长时间t3 。
答案:(1)4N(2)42m(3)2.1s
[解析](1)第一次飞行中,设加速度为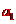
 匀加速运动
匀加速运动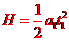
由牛顿第二定律
解得
(2)第二次飞行中,设失去升力时的速度为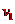 ,上升的高度为
,上升的高度为
匀加速运动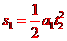
设失去升力后的速度为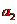 ,上升的高度为
,上升的高度为
由牛顿第二定律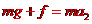
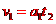

解得
(3)设失去升力下降阶段加速度为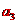 ;恢复升力后加速度为
;恢复升力后加速度为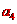 ,恢复升力时速度为
,恢复升力时速度为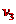
由牛顿第二定律 
F+f-mg=ma4
且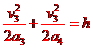
V3=a3t3
解得t3= (s)(或2.1s)
(s)(或2.1s)
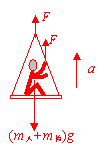
13、(2009年安徽卷)22.在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚忍不拔的意志和自强不息的精神。为了探究上升过程中运动员与绳索和吊椅间的作用,可将过程简化。一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦。重力加速度取g=10m/s2。当运动员与吊椅一起正以加速度a=1m/s2上升时,
试求
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力。
 答案:440N,275N
答案:440N,275N
 解析:解法一:(1)设运动员受到绳向上的拉力为F,由于跨过定滑轮的两段绳子拉力相等,吊椅受到绳的拉力也是F。对运动员和吊椅整体进行受力分析如图所示,则有:
解析:解法一:(1)设运动员受到绳向上的拉力为F,由于跨过定滑轮的两段绳子拉力相等,吊椅受到绳的拉力也是F。对运动员和吊椅整体进行受力分析如图所示,则有:



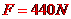
 由牛顿第三定律,运动员竖直向下拉绳的力
由牛顿第三定律,运动员竖直向下拉绳的力
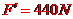
 (2)设吊椅对运动员的支持力为FN,对运动员进行受力分析如图所示,则有:
(2)设吊椅对运动员的支持力为FN,对运动员进行受力分析如图所示,则有:
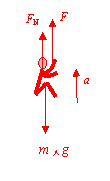



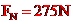
 由牛顿第三定律,运动员对吊椅的压力也为275N
由牛顿第三定律,运动员对吊椅的压力也为275N
 解法二:设运动员和吊椅的质量分别为M和m;运动员竖直向下的拉力为F,对吊椅的压力大小为FN。
解法二:设运动员和吊椅的质量分别为M和m;运动员竖直向下的拉力为F,对吊椅的压力大小为FN。
 根据牛顿第三定律,绳对运动员的拉力大小为F,吊椅对运动员的支持力为FN。分别以运动员和吊椅为研究对象,根据牛顿第二定律
根据牛顿第三定律,绳对运动员的拉力大小为F,吊椅对运动员的支持力为FN。分别以运动员和吊椅为研究对象,根据牛顿第二定律

 ①
①

 ②
②
 由①②得
由①②得 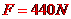


12、 (2009年山东卷)24.如图所示,某货场而将质量为m1=100 kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R=1.8 m。地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2=100 kg,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为
(2009年山东卷)24.如图所示,某货场而将质量为m1=100 kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R=1.8 m。地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2=100 kg,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为 1,木板与地面间的动摩擦因数
1,木板与地面间的动摩擦因数 =0.2。(最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s2)
=0.2。(最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s2)
(1)求货物到达圆轨道末端时对轨道的压力。
(2)若货物滑上木板4时,木板不动,而滑上木板B时,木板B开始滑动,求 1应满足的条件。
1应满足的条件。
(3)若 1=0。5,求货物滑到木板A末端时的速度和在木板A上运动的时间。
1=0。5,求货物滑到木板A末端时的速度和在木板A上运动的时间。
答案:(1)3000N;(2) ;(3)0.4s
;(3)0.4s
解析:(1)设货物滑到圆轨道末端是的速度为v0,对货物的下滑过程中根据机械能守恒定律得, ①,
①,
设货物在轨道末端所受支持力的大小为FN,根据牛顿第二定律得, ②,
②,
联立以上两式代入数据得FN=3000N③,
根据牛顿第三定律,货物到达圆轨道末端时对轨道的压力大小为3000N,方向竖直向下。
(2)若滑上木板A时,木板不动,由受力分析得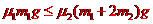 ④,
④,
若滑上木板B时,木板B开始滑动,由受力分析得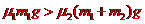 ⑤,
⑤,
联立④⑤式代入数据得 ⑥。
⑥。
(3)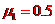 ,由⑥式可知,货物在木板A上滑动时,木板不动。设货物在木板A上做减速运动时的加速度大小为a1,由牛顿第二定律得
,由⑥式可知,货物在木板A上滑动时,木板不动。设货物在木板A上做减速运动时的加速度大小为a1,由牛顿第二定律得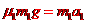 ⑦,
⑦,
设货物滑到木板A末端是的速度为v1,由运动学公式得 ⑧,
⑧,
联立①⑦⑧式代入数据得v1=4m/s⑨,
 设在木板A上运动的时间为t,由运动学公式得v1=v0-a1t⑩,联立①⑦⑨⑩式代入数据得t=0.4s。
设在木板A上运动的时间为t,由运动学公式得v1=v0-a1t⑩,联立①⑦⑨⑩式代入数据得t=0.4s。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com