2．功能观点：首先对带电体受力分析，再分析运动形式，然后根据具体情况选用相应公式计算．

(1)若选用动能定理，则要分清有多少个力做功，是恒力做功还是变力做功，同时要明确初、末状态及运动过程中的动能的增量．

(2)若选用能量守恒定律，则要分清带电体在运动中共有多少种能量参与转化，哪些能量是增加的，哪些能量是减少的．

例3　如图7所示，A、B为半径R＝1 m的四分之一光滑绝缘竖直圆弧轨道，在四分之一圆弧区域内存在着E＝1×10⁶ V/m、竖直向上的匀强电场，有一质量m＝1 kg、带电量q＝＋1.4×10^－5 C的物体(可视为质点)，从A点的正上方距离A点H处由静止开始自由下落(不计空气阻力)，BC段为长L＝2 m、与物体间动摩擦因数为μ＝0.2的粗糙绝缘水平面，CD段为倾角θ＝53°且离地面DE高h＝0.8 m的斜面．(取g＝10 m/s²)

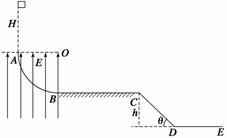
图7

(1)若H＝1 m，物体能沿轨道AB到达最低点B，求它到达B点时对轨道的压力大小；

(2)通过你的计算判断：是否存在某一H值，能使物体沿轨道AB经过最低点B后最终停在距离B点0.8 m处；

(3)若高度H满足：0.85 m≤H≤1 m，请通过计算表示出物体从C处射出后打到的范围．(已知sin 53°＝0.8，cos 53°＝0.6.不需要计算过程，但要有具体的位置，不讨论物体反弹以后的情况)

审题与关联

解析　(1)物体由初始位置运动到B点的过程中根据动能定理有mg(R＋H)－qER＝mv

到达B点时由支持力F_N、重力、电场力的合力提供向心力F_N－mg＋qE＝m，解得F_N＝8 N

根据牛顿第三定律，可知物体对轨道的压力大小为8 N，方向竖直向下

(2)要使物体沿轨道AB到达最低点B，当支持力为0时，最低点有个最小速度v，则qE－mg＝m

解得v＝2 m/s

在粗糙水平面上，由动能定理得：－μmgx＝－mv²，所以x＝1 m>0.8 m

故不存在某一H值，使物体沿着轨道AB经过最低点B后，停在距离B点0.8 m处．

(3)在斜面上距离D点 m范围内(如图PD之间区域)

在水平面上距离D点0.2 m范围内(如图DQ之间区域)

答案　(1)8 N　(2)不存在　(3)在斜面上距离D点 m范围内　在水平面上距离D点0.2 m范围内

突破训练3　如图8所示，在竖直平面内，AB为水平放置的绝缘粗糙轨道，CD为竖直放置的足够长绝缘粗糙轨道，AB与CD通过四分之一绝缘光滑圆弧形轨道平滑连接，圆弧的圆心为O，半径R＝0.50 m，轨道所在空间存在水平向右的匀强电场，电场强度的大小E＝1.0×10⁴ N/C，现有质量m＝0.20 kg，电荷量q＝8.0×10^－4 C的带电体(可视为质点)，从A点由静止开始运动，已知s_AB＝1.0 m，带电体与轨道AB、CD间的动摩擦因数均为0.5.假定带电体与轨道之间的最大静摩擦力和滑动摩擦力相等．求：(取g＝10 m/s²)

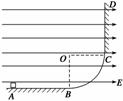
图8

(1)带电体运动到圆弧形轨道C点时的速度；

(2)带电体最终停在何处．

答案　(1)10 m/s　(2)到C点的竖直距离为 m处

解析　(1)设带电体到达C点时的速度为v，从A到C由动能定理得：qE(s_AB＋R)－μmgs_AB－mgR＝mv²

解得v＝10 m/s

(2)设带电体沿竖直轨道CD上升的最大高度为h，从C到D由动能定理得：

－mgh－μqEh＝0－mv²

解得h＝ m

在最高点，带电体受到的最大静摩擦力Ffmax＝μqE＝4 N，

重力G＝mg＝2 N

因为G<F_fmax

所以带电体最终静止在到C点的竖直距离为 m处．

(限时：45分钟)

►题组1　示波管的原理与应用

1．动力学观点

动力学观点是指用匀变速运动的公式来解决实际问题，一般有两种情况：

(1)带电粒子初速度方向与电场线共线，则粒子做匀变速直线运动；

(2)带电粒子的初速度方向垂直电场线，则粒子做匀变速曲线运动(类平抛运动)．当带电粒子在电场中做匀变速曲线运动时，一般要采用类平抛运动规律解决问题．

32．综合运用动力学观点和功能观点解决带

电体在电场中的运动

3．此类题型一般有三种情况：一是粒子做单向直线运动(一般用牛顿运动定律求解)，二是粒子做往返运动(一般分段研究)，三是粒子做偏转运动(一般根据交变电场的特点分段研究)．

例2　如图5(a)所示，A、B为两块平行金属板，极板间电压为U_AB＝1 125 V，板中央有小孔O和O′.现有足够多的电子源源不断地从小孔O由静止进入A、B之间．在B板右侧，平行金属板M、N长L₁＝4×10^－2 m，板间距离d＝4×10^－3 m，在距离M、N右侧边缘L₂＝0.1 m处有一荧光屏P，当M、N之间未加电压时电子沿M板的下边沿穿过，打在荧光屏上的O″并发出荧光．现给金属板M、N之间加一个如图(b)所示的变化电压u₁，在电压变化时，M板电势低于N板．已知电子质量为m_e＝9.0×10^－31 kg，电量为e＝1.6×10^－19C.

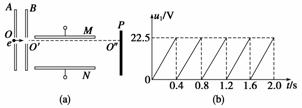
图5

(1)每个电子从B板上的小孔O′射出时的速度多大？

(2)打在荧光屏上的电子范围是多少？

(3)打在荧光屏上的电子的最大动能是多少？

解析　(1)电子经A、B两块金属板加速，有：U_AB＝mv

得v₀＝ ＝ m/s＝2×10⁷ m/s

(2)电子通过极板的时间为t＝L₁/v₀＝2×10^－9 s，远小于电压变化的周期，故电子通过极板时可认为板间电压不变．

当μ₁＝22.5 V时，电子经过M、N极板向下的偏移量最大，为y₁＝··²＝×ײ m＝2×10^－3 m

y₁<d，说明所有的电子都可以飞出M、N[来源:学#科#网]

此时电子射出极板后在竖直方向的速度大小为

v_y＝·＝× m/s＝2×10⁶ m/s

电子射出极板MN后到达荧光屏P的时间为：

t₂＝＝ s＝5×10^－9 s

电子射出极板MN后到达荧光屏P的偏移量为

y₂＝v_yt₂＝2×10⁶×5×10^－9 m＝0.01 m

电子打在荧光屏P上的总偏移量为：

y＝y₁＋y₂＝0.012 m，方向竖直向下；

打在荧光屏上的电子范围是：从O″竖直向下0～0.012 m.

(3)当u₁＝22.5 V时，电子飞出电场的动能最大，

E_K＝m(v＋v)＝×9×10^－31[(2×10⁷)²＋(2×10⁶)²]≈1.82×10^－16 J.

答案　见解析

当电压周期性变化时，由E＝知，电场强度E也周期性变化，由F＝qE知电场力F周期性变化，由a＝知加速度a与电压变化图象形状相同，画出v－t图象则可以分析粒子运动特点．

突破训练2　在金属板A、B间加上如图6乙所示的大小不变、方向周期性变化的交变电压，其周期为T.现有电子以平行于金属板的速度v₀从两板中央射入(如图甲所示)．已知电子的质量为m，电荷量为e，不计电子的重力，求：

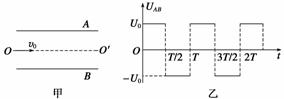
图6

(1)若电子从t＝0时刻射入，在半个周期内恰好能从A板的边缘飞出，则电子飞出时速度的大小为多少？

(2)若电子从t＝0时刻射入，恰能平行于金属板飞出，则金属板至少为多长？

(3)若电子恰能从两板中央平行于板飞出，电子应从哪一时刻射入？两板间距至少为多大？

答案　(1) 　(2)v₀T

(3)＋k·(k＝0,1,2，…)　T

解析　(1)由动能定理得：e·＝mv²－mv

解得v＝ .

(2)t＝0时刻射入的电子，在垂直于极板方向上做匀加速运动，向正极板方向偏转，半个周期后电场方向反向，则继续在该方向上做匀减速运动，再经过半个周期，电场方向上的速度减到零，实际速度等于初速度v₀，平行于极板，以后继续重复这样的运动．

要使电子恰能平行于金属板飞出，则在OO′方向上至少运动一个周期，故极板长至少为L＝v₀T.

(3)若要使电子从极板中央平行于极板飞出，则电子在电场方向上应先加速、再减速，反向加速再减速，每段时间相同，一个周期后恰好回到OO′线．所以应在t＝＋k·(k＝0,1,2，…)时射入．

极板间距离要求满足在加速、减速阶段电子不打到极板上．

由牛顿第二定律有a＝.

加速阶段运动的距离s＝··()²≤

可解得d≥T

故两板间距至少为T

2．分析时从两条思路出发：一是力和运动的关系，根据牛顿第二定律及运动学规律分析；二是功能关系．

1．注重全面分析(分析受力特点和运动规律)，抓住粒子的运动具有周期性和在空间上具有对称性的特征，求解粒子运动过程中的速度、位移、做功或确定与物理过程相关的边界条件．

2．工作原理

偏转电极XX′和YY′不加电压，电子打到屏幕中心；若只在XX′之间加电压，电子只在X方向偏转；若只在YY′之间加电压，电子只在Y方向偏转；若XX′加扫描电压，YY′加信号电压，屏上会出现随信号而变化的图象．

例1　(2011·安徽·18)图2为示波管的原理图，如果在电极YY′之间所加的电压按图3甲所示的规律变化，在电极XX′之间所加的电压按图乙所示的规律变化，则在荧光屏上会看到的图形是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

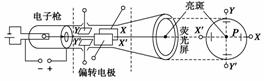
图2

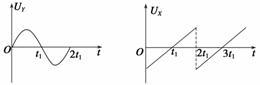
甲　　　　　　乙

图3

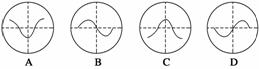
解析　由图甲及图乙知，当U_Y为正时，Y板电势高，电子向Y偏，而此时U_X为负，即X′板电势高，电子向X′板偏，所以选B.

答案　B

　　　示波管荧光屏上图线形状的判断方法

示波管中的电子在YY′和XX′两个偏转电极作用下，同时参与两个类平抛运动，一方面沿YY′方向偏转，另一方面沿XX′方向偏转，找出几个特殊点，即可确定荧光屏上的图形．

突破训练1　示波管是示波器的核心部件，它由电子枪、偏转电极和荧光屏组成，如图4所示．如果在荧光屏上P点出现亮斑，那么示波管中的　　　　　　　　　　 　　　　　　　 (　)

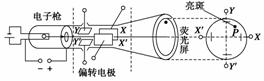
图4

A．极板X应带正电

B．极板X′应带正电

C．极板Y应带正电

D．极板Y′应带正电

答案　AC

解析　根据亮斑的位置，电子偏向XY区间，说明电子受到电场力作用发生了偏转，因此极板X、极板Y均应带正电．

考点二　带电粒子在交变电场中的运动

1．构造及功能(如图1所示)

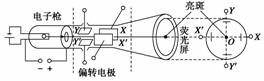
图1

(1)电子枪：发射并加速电子．

(2)偏转电极YY′：使电子束竖直偏转(加信号电压)；偏转电极XX′：使电子束水平偏转(加扫描电压)．

26、（1）400N （2分）　　 （2）10⁴Pa　 （2分）

　 （3）4800J（2分）　　 （4）80W（2分）

四、计算题

25、4N（2分）　 物体在水中静止时，漂浮在水面，所以浮力等于物体重力，F_浮＝G=3N　 （2分）