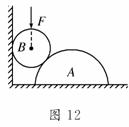
2.在粗糙水平地面上与墙平行放着一个截面为半圆的柱状物体A，A与竖直墙之间放一光滑圆球B，整个装置处于静止状态．现对B施加一竖直向下的力F，F的作用线通过球心，设墙对B的作用力为F₁，A对B的作用力为F₂，地面对A的作用力为F₃，若F缓慢增大而整个装置仍保持静止，截面如图12所示，在此过程中　　 (　)

A．F₁保持不变，F₃缓慢增大　 B．F₁缓慢增大，F₃保持不变

C．F₂缓慢增大，F₃缓慢增大　 D．F₂缓慢增大，F₃保持不变

一、选择题

1.下列说法中正确的是(　)

A.加速度增大，速度一定增大

B.速度的改变量Δv越大，加速度就越大

C.物体有加速度，速度就增大

D.速度很大的物体，其加速度可以很小

8．如图8所示，AB是一倾角为θ＝37°的绝缘粗糙直轨道，滑块与斜面间的动摩擦因数μ＝0.30，BCD是半径为R＝0.2 m的光滑圆弧轨道，它们相切于B点，C为圆弧轨道的最低点，整个空间存在着竖直向上的匀强电场，场强E＝4.0×10³ N/C，质量m＝0.20 kg的带电滑块从斜面顶端由静止开始滑下．已知斜面AB对应的高度h＝0.24 m，滑块带电荷量q＝－5.0×10^－4 C，取重力加速度g＝10 m/s²，sin 37°＝0.60，cos 37°＝0.80.求：

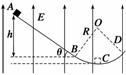
图8

(1)滑块从斜面最高点滑到斜面底端B点时的速度大小；

(2)滑块滑到圆弧轨道最低点C时对轨道的压力．

答案　(1)2.4 m/s　(2)11.36 N，方向竖直向下

解析　(1)滑块沿斜面滑下的过程中，受到的滑动摩擦力

F_f＝μ(mg＋qE)cos 37°＝0.96 N

设到达斜面底端时的速度为v₁，根据动能定理得

(mg＋qE)h－F_f＝mv

解得v₁＝2.4 m/s

(2)滑块从B到C，由动能定理可得：

(mg＋qE)R(1－cos 37°)＝mv－mv

当滑块经过最低点C时，有F_N－(mg＋qE)＝m

由牛顿第三定律：F_N′＝F_N

解得：F_N′＝11.36 N，方向竖直向下．

7．在真空中存在空间范围足够大的、水平向右的匀强电场．若将一个质量为m、带正电、电荷量为q的小球在此电场中由静止释放，小球将沿与竖直方向夹角为53°的直线运动．现将该小球从电场中某点以初速度v₀竖直向上抛出，求运动过程中(sin 53°＝0.8)

(1)此电场的电场强度大小；

(2)小球运动的抛出点至最高点之间的电势差U；

(3)小球的最小动能．

答案　见解析

解析　(1)根据题设条件，电场力大小

F＝mgtan 53°＝mg＝qE，解得E＝

(2)上抛小球沿竖直方向做匀减速运动，在竖直方向的速度为v_y＝v₀－gt

沿水平方向做初速度为0的匀加速运动，加速度为a_x＝＝g

小球上升到最高点的时间t＝，此过程小球沿电场方向位移：x＝a_xt²＝

电场力做功W＝Fx＝mv

小球运动的抛出点至最高点之间的电势差U＝mv

(3)水平速度v_x＝a_xt，竖直速度v_y＝v₀－gt，小球的速度v＝

由以上各式得出v²＝g²t²－2v₀gt＋v

解得当t＝时，v有最小值v_min＝v₀，小球动能的最小值为E_min＝mv＝mv.

6．在一个水平面上建立x轴，在过原点O右侧空间有一个匀强电场，电场强度大小E＝6×

10⁵ N/C，方向与x轴正方向相同，在O处放一个电荷量q＝5×10^－8 C、质量m＝0.010 kg的带负电绝缘物块，物块与水平面间的动摩擦因数μ＝0.2，沿x轴正方向给物块一个初速度v₀＝2 m/s，如图7所示，(g取10 m/s²)求：

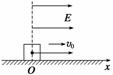
图7

(1)物块最终停止时的位置；

(2)物块在电场中运动过程的机械能增量．

答案　(1)原点O左侧0.2 m处　(2)－0.016 J

解析　(1)第一个过程：物块向右做匀减速运动到速度为零．

F_f＝μmg

F＝qE

由牛顿第二定律得F_f＋F＝ma

由运动学公式得2ax₁＝v

解得x₁＝0.4 m

第二个过程：物块向左做匀加速运动，离开电场后再做匀减速运动直到停止．由动能定理得：Fx₁－F_f(x₁＋x₂)＝0

得x₂＝0.2 m，则物块停止在原点O左侧0.2 m处．

(2)物块在电场中运动过程的机械能增量

ΔE＝W_f＝－2μmgx₁＝－0.016 J.

5．空间某区域内存在着电场，电场线在竖直平面上的分布如图6所示．一个质量为m、电荷量为q的带电小球在该电场中运动，小球经过A点时的速度大小为v₁，方向水平向右；运动至B点时的速度大小为v₂，运动方向与水平方向之间的夹角为α，A、B两点间的高度差为h、水平距离为s，则以下判断正确的是　　　　　　　　　　　　　　　　　　　　 (　)

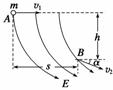
图6

A．A、B两点的电场强度和电势关系为E_A<E_B、φ_A<φ_B

B．如果v₂>v₁，则电场力一定做正功

C．A、B两点间的电势差为(v－v)

D．小球从A点运动到B点的过程中电场力做的功为mv－mv－mgh

答案　D

解析　由电场线的方向和疏密可知A点电场强度小于B点，但A点电势高于B点，A错误．若v₂>v₁说明合外力对小球做正功，但电场力不一定做正功，B错误．由于有重力做功，A、B两点间电势差不是(v－v)，C错误．小球从A点运动到B点过程中由动能定理得W_电＋mgh＝mv－mv，所以W_电＝mv－mv－mgh，D正确．

4．如图5甲所示，在y＝0和y＝2 m之间有沿着x轴方向的匀强电场，MN为电场区域的上边界，在x轴方向范围足够大．电场强度的变化如图乙所示，取x轴正方向为电场正方向，现有一个带负电的粒子，粒子的比荷为＝1.0×10^－2 C/kg，在t＝0时刻以速度v₀＝5×10² m/s从O点沿y轴正方向进入电场区域，不计粒子重力．求：

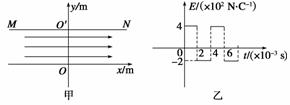
图5

(1)粒子通过电场区域的时间；

(2)粒子离开电场时的位置坐标；

(3)粒子通过电场区域后沿x方向的速度大小．

答案　(1)4×10^－3 s　(2)(－2×10^－5 m,2 m)

(3)4×10^－3 m/s

解析　(1)因粒子初速度方向垂直电场方向，在电场中做类平抛运动，所以粒子通过电场区域的时间

t＝＝4×10^－3 s

(2)粒子沿x轴负方向先加速后减速，加速时的加速度大小为a₁＝＝4 m/s²，减速时的加速度大小为a₂＝＝2 m/s²由运动学规律得

x方向上的位移为

x＝a₁()²＋a₁()²－a₂()²＝2×10^－5 m

因此粒子离开电场时的位置坐标为(－2×10^－5 m,2 m)

(3)粒子通过电场区域后沿x方向的速度为v_x＝a₁－a₂＝4×10^－3 m/s

►题组3　用动力学和功能观点分析带电体在电场中的运动

3．(2011·安徽·20)如图4(a)所示，两平行正对的金属板A、B间加有如图(b)所示的交变电压，一重力可忽略不计的带正电粒子被固定在两板的正中间P处．若在t₀时刻释放该粒子，粒子会时而向A板运动，时而向B板运动，并最终打在A板上．则t₀可能属于的时间段是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

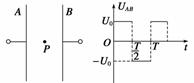
(a)　　　　(b)

图4

A．0<t₀<　 　　　　　　　　　　　 B.<t₀<

C.<t₀<T　 　　　　　　　　　　　 D．T<t₀<

答案　B

解析　设粒子的速度方向、位移方向向右为正．依题意得，粒子的速度方向时而为正，时而为负，最终打在A板上时位移为负，速度方向为负．

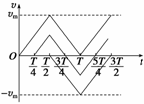
作出t₀＝0、、、时粒子运动的速度图象如图所示．由于速度图线与时间轴所围面积表示粒子通过的位移，则由图象可知0<t₀<，<t₀<T时粒子在一个周期内的总位移大于零；<t₀<时粒子在一个周期内的总位移小于零；当t₀>T时情况类似．因粒子最终打在A板上，则要求粒子在每个周期内的总位移应小于零，对照各选项可知只有B正确．

2．如图3甲所示，两平行金属板竖直放置，左极板接地，中间有小孔，右极板电势随时间变化的规律如图乙所示，电子原来静止在左极板小孔处，不计电子的重力，下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

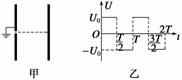
图3

A．若t＝0时刻释放电子，电子始终向右运动，直到打到右极板上

B．若t＝0时刻释放电子，电子可能在两板间振动

C．若t＝T/4时刻释放电子，电子可能在两板间振动，也可能打到右极板上

D．若t＝3T/8时刻释放电子，电子必然打到左极板上

答案　AC

解析　若t＝0时刻释放电子，电子将重复先加速后减速的运动，直到打到右极板，不会在两板间振动，所以A正确，B错；若从t＝T/4时刻释放电子，电子先加速T/4，再减速T/4，有可能电子已到达右极板，若此时未到达右极板，则电子将在两极板间振动，所以C正确；同理，若从t＝3T/8时刻释放电子，电子有可能达到右极板，也有可能从左极板射出，这取决于两板间的距离，所以D项错误；此题考查带电粒子在交变电场中的运动．

1．如图1所示为示波管构造的示意图，现在XX′间加上U_xx′－t信号，YY′间加上U_yy′－t信号，(如图2甲、乙所示)．则在屏幕上看到的图形是　　　　　　　　　　　　　　　　　 (　)

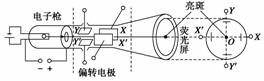
图1

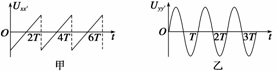
图2

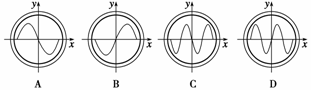
答案　D

解析　沿电场方向带电粒子做加速运动，在垂直电场方向带电粒子做匀速运动，粒子经过竖直的YY′(信号电压)电场偏转，再经过水平的XX′(扫描电压)电场偏转，最后在显示屏上形成稳定的图象．在甲图中开始U_xx′<0，乙图中开始U_yy′＝0之后大于0，由此排除B、C项.0～T在x方向电子恰好从－x处到屏中央，在y方向完成一次扫描，T～2T水平方向电子从中央向x正向移动，在y方向再完成一次扫描．所以本题D项正确．

►题组2　带电粒子在交变电场中的运动