
A.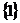 B.
B.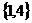 C.
C. D.
D.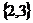
1、 已知全集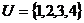 ,集合
,集合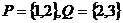 ,则
,则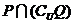 等于
等于
又 平面
平面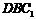 ,
,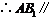 平面
平面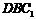 .
.
点评:平面的法向量是空间向量的一个重要概念,它在解决立体几何的许多问题中都有很好的应用.
由于

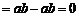 ,得
,得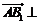
 .
.
不妨令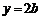 ,则
,则
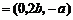 .
.
则 所以
所以
设平面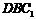 的一个法向量为
的一个法向量为
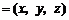 ,
,
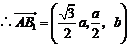 ,
,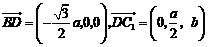 .
.
证明:建立如图所示的空间直角坐标系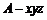 .设正三棱柱的底面边长为
.设正三棱柱的底面边长为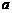 ,侧棱长为
,侧棱长为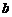 ,则
,则 ,
,
点评:向量法求二面角是一种独特的方法,因为它不但是传统方法的有力补充,而且还可以另辟溪径,解决传统方法难以解决的求二面角问题.向量法求二面角通常有以下三种转化方式:①先作、证二面角的平面角 ,再求得二面角的大小为
,再求得二面角的大小为 ;②先求二面角两个半平面的法向量
;②先求二面角两个半平面的法向量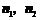 (注意法向量的方向要分布在二面角的内外),再求得二面角的大小为
(注意法向量的方向要分布在二面角的内外),再求得二面角的大小为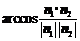 或其补角;③先分别在二面角两个半平面内作棱的垂线(垂足不重合),又可转化为求两条异面直线的夹角.
或其补角;③先分别在二面角两个半平面内作棱的垂线(垂足不重合),又可转化为求两条异面直线的夹角.
例题15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com