3．[动力学中的图象问题]一个木块以某一水平初速度自由滑上粗糙的水平面，在水平面上运动的v－t图象如图1所示．已知重力加速度为g，则根据图象不能求出的物理量是

(　)

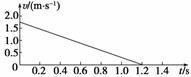
图1

A．木块的位移

B．木块的加速度

C．木块所受摩擦力

D．木块与桌面间的动摩擦因数

答案　C

解析　位移可由图象与时间轴所围的面积求出，由v－t图线的斜率可求出加速度a，由牛顿第二定律知，a＝μg，故动摩擦因数μ也可求出，由于不知木块的质量，故不能求出木块所受摩擦力．

2．[超重与失重概念的应用]下列说法中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．体操运动员双手握住单杠吊在空中不动时处于失重状态

B．蹦床运动员在空中上升和下落过程中都处于失重状态

C．举重运动员在举起杠铃后不动的那段时间内处于超重状态

D．游泳运动员仰卧在水面静止不动时处于失重状态

答案　B

解析　当加速度有竖直向下的分量时，物体处于失重状态；当加速度有竖直向上的分量时，物体处于超重状态，蹦床运动员在空中上升和下降的过程中加速度方向均竖直向下，且a＝g，为完全失重状态，所以B正确．而A、C、D中运动员均为平衡状态，F＝mg，既不超重也不失重．

1．[对超重和失重的理解]关于超重和失重的下列说法中，正确的是　　　　　　　　　　　　 (　)

A．超重就是物体所受的重力增大了，失重就是物体所受的重力减小了

B．物体做自由落体运动时处于完全失重状态，所以做自由落体运动的物体不受重力作用

C．物体具有向上的速度时处于超重状态，物体具有向下的速度时处于失重状态

D．物体处于超重或失重状态时，物体的重力始终存在且不发生变化

答案　D

解析　物体具有向上的加速度时处于超重状态，具有向下的加速度时处于失重状态，超重和失重并非物体的重力发生变化，而是物体对支持物的压力或对悬挂物的拉力发生了变化，综上所述，A、B、C均错，D正确．

12．在如图10所示的装置中，两物体通过一段绳与两个滑轮连在一起，质量分别为m₁、m₂，悬点a、b间的距离远大于滑轮的直径，不计一切摩擦，整个装置处于静止状态．由图可知　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

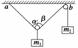
图10

A．α一定等于β　 　　　　　　　　　　　　　　 B．m₁一定大于m₂

C．m₁一定小于2m₂　 　　　　　　　　　　　 D．m₁可能大于2m₂

答案　AC

解析　滑轮两侧绳的拉力大小相等，合力竖直向上，所以A正确；滑轮两侧绳的拉力大小等于m₂g，其合力大小等于m₁g.当滑轮两侧的绳竖直向上时m₂最小，等于m₁的一半，因滑轮两侧的绳不可能竖直向上，所以C正确，B、D错误．

11．如图9所示，杆BC的B端用铰链固定在竖直墙上，另一端C为一滑轮．重物G上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙缓慢向下移(BC杆、滑轮、绳的质量及摩擦均不计)，则　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

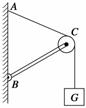
图9

A．绳的拉力增大，BC杆受绳的压力增大

B．绳的拉力不变，BC杆受绳的压力增大

C．绳的拉力不变，BC杆受绳的压力减小

D．绳的拉力不变，BC杆受绳的压力不变

答案　B

解析　选取绳子与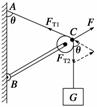滑轮的接触点为研究对象，对其受力分析，如图所

示．绳中的弹力大小相等，即F_T1＝F_T2＝G，C点处于三力平衡状态，

将三个力的示意图平移可以组成闭合三角形，如图中虚线所示，设

AC段绳子与竖直墙壁间的夹角为θ，则根据几何知识可知F＝2G

sin ，当绳的A端沿墙缓慢向下移时，绳的拉力不变，θ增大，F也增大，根据牛顿第

三定律知，BC杆受绳的压力增大，B正确．

10．如图8所示，质量为m的物体悬挂在轻质支架上，斜梁OB与竖直方向的夹角为θ.设水平横梁OA和斜梁OB作用于O点的弹力分别为F₁和F₂，以下结果正确的是 (　)

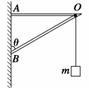
图8

A．F₁＝mgsin θ

B．F₁＝

C．F₂＝mgcos θ

D．F₂＝

答案　D

解析　由题可知，对悬挂的物体由力的平衡条件可知绳子的拉力等

于物体的重力，则绳子拉O点的力也等于物体的重力．求OA和OB

的弹力，选择的研究对象为作用点O，受力分析如图，由平衡条件

可知，F₁和F₂的合力与F_T等大反向，则由平行四边形定则和几何关系可得：

F₁＝mgtan θ，F₂＝，故D正确．

9．三个质量均为1 kg的相同木块a、b、c和两个劲度系数均为500 N/m的相同轻弹簧p、q

用轻绳连接，如图7所示，其中a放在光滑水平桌面上．开始时p弹簧处于原长，木块

都处于静止状态．现用水平力F缓慢地向左拉p弹簧的左端，直到c木块刚好离开水平

地面为止，g取10 m/s².该过程p弹簧的左端向左移动的距离是　　　　　　　　　　　　 (　)

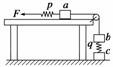
图7

A．4 cm　 　　　　　　 B．6 cm　 　　　　　　 C．8 cm　 　　　　　　 D．10 cm

答案　C

解析　“缓慢地拉动”说明系统始终处于平衡状态，该过程中p弹簧的左端向左移动的距离等于两个弹簧长度变化量之和；最初，p弹簧处于原长，而q弹簧受到竖直向下的压力F₁＝m_bg＝1×10 N＝10 N，所以其压缩量为x₁＝F₁/k＝2 cm；最终c木块刚好离开水平地面，q弹簧受到竖直向下的拉力F₂＝m_cg＝1×10 N＝10 N，其伸长量为x₂＝F₂/k＝2 cm，拉力F＝(m_b＋m_c)g＝2×10 N＝20 N，p弹簧的伸长量为x₃＝F/k＝4 cm，所以所求距离x＝x₁＋x₂＋x₃＝8 cm.

►题组4　“滑轮”模型和“死结”模型问题

8．如图6所示，两木块的质量分别为m₁和m₂，两轻质弹簧的劲度系数分别为k₁和k₂，上

面木块压在上面弹簧上(但不拴接)，整个系统处于平衡状态．现缓慢向上提上面的木块，

直到它刚离开上面的弹簧．在此过程中下面木块移动的距离为　　　　　　　　　　　　 (　)

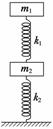
图6

A.　 　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　 D.

答案　C

解析　在没有施加外力向上提时，弹簧k₂被压缩，压缩的长度为：Δx＝.在用力缓慢向上提m₁直至m₁刚离开上面弹簧时，弹簧k₂仍被压缩，压缩量为Δx′＝.所以在此过程中，下面木块移动的距离为：Δx－Δx′＝，故选C.

7．如图5所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量m＝30 kg，人的质量M＝50 kg，g取10 m/s².试求：

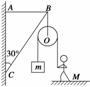
图5

(1)此时地面对人的支持力的大小；

(2)轻杆BC和绳AB所受力的大小．

答案　(1)200 N　(2)400 N　200 N

解析　(1)因匀速提起重物，则F_T＝mg，故绳对人的拉力也为mg，所以地面对人的支持力为：

F_N＝Mg－mg＝(50－30)×10 N＝200 N，方向竖直向上．

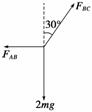(2)定滑轮对B点的拉力方向竖直向下，大小为2mg，杆对B点的弹力

方向沿杆，如图所示，由共点力平衡条件得：

F_AB＝2mgtan 30°＝2×30×10× N＝200 N

F_BC＝＝ N＝400 N.

►题组3　弹簧的弹力的分析与计算

6．叠罗汉是一种二人以上层层叠成各种造型的游戏形式，也是一种高难度的杂技．图4所示为六人叠成的三层静态造型，假设每个人的重量均为G，下面五人的背部均呈水平状态，则最底层正中间的人的一只脚对水平地面的压力约为　　 　　　　　　　　　　　　　　 (　)

图4

A.G　 　　　　　　　　 B.G　　　　　　　　　　 C.G　 　　　　　　　　 D.G

答案　C

解析　下层中间人背上受力为：F＝3G×＝G，所以他的一只脚对地压力为：F′＝(F＋G)×＝G，C正确．