2．如图1所示是某同学站在力传感器上做下蹲—起立的动作时记录的压力F随时间t变化的图线，由图线可知该同学　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

图1

A．体重约为650 N

B．做了两次下蹲—起立的动作

C．做了一次下蹲—起立的动作，且下蹲后约2 s起立

D．下蹲过程中先处于超重状态后处于失重状态

答案　AC

解析　做下蹲—起立的动作时，下蹲过程中先向下加速后向下减速，因此先处于失重状态后处于超重状态，D错误；由图线可知，第一次下蹲4 s末结束，到6 s末开始起立，所以A、C正确，B错误．

1．有关超重和失重，以下说法中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．物体处于超重状态时，所受重力增大，处于失重状态时，所受重力减小

B．竖直上抛的木箱中的物体处于完全失重状态

C．在沿竖直方向运动的升降机中出现失重现象时，升降机必定处于下降过程

D．站在月球表面的人处于失重状态

答案　B

解析　超重与失重时，物体自身的重力不会发生变化，A项错；竖直上抛中的木箱中的物体的加速度都为竖直向下的重力加速度g，所以是完全失重，B项正确；升降机失重时，也有可能是做向上的减速运动，C项错；月球表面对人体也有引力作用，虽然他对月面的压力小于在地球时对地球表面的压力，但对月面的压力等于他在月球上受的重力，所以这不是失重，D项错，正确选项为B.

3．如图12所示，为皮带传输装置示意图的一部分，传送带与水平地面的倾角θ＝37°，A、B两端相距5.0 m，质量为M＝10 kg的物体以v₀＝6.0 m/s的速度沿AB方向从A端滑上传送带，物体与传送带间的动摩擦因数处处相同，均为0.5.传送带顺时针运转的速度v＝4.0 m/s，(g取10 m/s²，sin 37°＝0.6，cos 37°＝0.8)求：

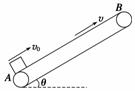
图12

(1)物体从A点到达B点所需的时间；

(2)若传送带顺时针运转的速度可以调节，物体从A点到达B点的最短时间是多少？

答案　(1)2.2 s　(2)1 s

解析　(1)设在AB上物体的速度大于v＝4.0 m/s时加速度大小为a₁，由牛顿第二定律得mgsin θ＋μmgcos θ＝ma₁

设经t₁速度与传送带速度相同，t₁＝

通过的位移x₁＝

设速度小于v时物体的加速度为a₂

mgsin θ－μmgcos θ＝ma₂

物体继续减速，设经t₂速度到达传送带B点

L－x₁＝vt₂－a₂t

t＝t₁＋t₂＝2.2 s

(2)若传送带的速度较大，沿AB上滑时所受摩擦力一直沿皮带向上，则所用时间最短，此种情况加速度一直为a_{2[来源:学*科*网Z*X*X*K]}

L＝v₀t′－a₂t′²

t′＝1 s

(限时：30分钟)

►题组1　超重、失重的理解与应用

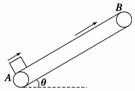
2．如图11所示，质量为m₁的足够长木板静止在光滑水平面上，其上放一质量为m₂的木块．t＝0时刻起，给木块施加一水平恒力F.分别用a₁、a₂和v₁、v₂表示木板、木块的加速度和速度大小，下列四个图中可能符合运动情况的是　　　　　 　　　　　　　　　　　　　　 (　)

图11

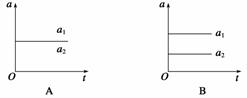
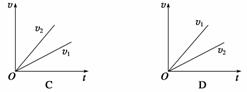
答案　AC

解析　若m₁和m₂在拉力F的作用下一起做匀加速直线运动，则a＝，选项A正确；若m₁和m₂在拉力F的作用下发生相对滑动，因为m₂的速度v₂大于m₁的速度v₁，所以选项C正确，D错误；又因v－t图象的斜率表示加速度，根据C图可知，a₂>a₁，选项B错误．

1．(2013·新课标Ⅱ·25)一长木板在水平地面上运动，在t＝0时刻将一相对于地面静止的物块轻放到木板上，以后木板运动的速度－时间图象如图10所示．已知物块与木板的质量相等，物块与木板间及木板与地面间均有摩擦．物块与木板间的最大静摩擦力等于滑动摩擦力，且物块始终在木板上．取重力加速度g＝10 m/s²，求：

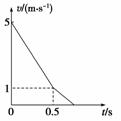
图10

(1)物块与木板间、木板与地面间的动摩擦因数；

(2)从t＝0时刻到物块与木板均停止运动时，物块相对于木板的位移的大小．

答案　(1)0.20　0.30　(2)1.125 m

解析　(1)从t＝0时开始，木板与物块之间的摩擦力使物块加速，使木板减速，此过程一直持续到物块和木块具有相同速度为止．

由题图可知，在t₁＝0.5 s时，物块和木板的速度相同．设t＝0到t＝t₁时间间隔内，物块和木板的加速度大小分别为a₁和a₂，则

a₁＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

a₂＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

式中v₀＝5 m/s、v₁＝1 m/s分别为木板在t＝0、t＝t₁时速度的大小．

设物块和木板的质量均为m，物块和木板间、木板与地面间的动摩擦因数分别为μ₁、μ₂，由牛顿第二定律得

μ₁mg＝ma₁ ③

(μ₁＋2μ₂)mg＝ma₂ ④

联立①②③④式得

μ₁＝0.20　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

μ₂＝0.30　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

(2)在t₁时刻后，地面对木板的摩擦力阻碍木板运动，物块与木板之间的摩擦力改变方向．设物块与木板之间的摩擦力大小为F_f，物块和木板的加速度大小分别为a₁′和a₂′，则由牛顿第二定律得

F_f＝ma₁′　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑦

2μ₂mg－F_f＝ma₂′　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑧

假设F_f＜μ₁mg，则a₁′＝a₂′；由⑤⑥⑦⑧式得

F_f＝μ₂mg＞μ₁mg，与假设矛盾，故F_f＝μ₁mg　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑨

由⑦⑨式知：物块加速度的大小a₁′等于a₁；物块的v－t图象如图中点划线所示．

由运动学公式可推知，物块和木板相对于地面的运动距离分别为

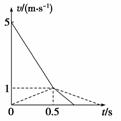
s₁＝2×　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑩

s₂＝t₁＋　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑪

物块相对于木板的位移的大小为

s＝s₂－s₁ ⑫

联立①⑤⑥⑧⑨⑩⑪⑫式得

s＝1.125 m

模拟题组

2．建模指导

解此类题的基本思路：(1)分析滑块和木板的受力情况，根据牛顿第二定律分别求出滑块和木板的加速度；(2)对滑块和木板进行运动情况分析，找出滑块和木板之间的位移关系或速度关系，建立方程．特别注意滑块和木板的位移都是相对地面的位移．

例5　如图9所示，质量M＝4.0 kg的长木板B静止在光滑的水平地面上，在其右端放一质量m＝1.0 kg的小滑块A(可视为质点)．初始时刻，A、B分别以v₀＝2.0 m/s向左、向右运动，最后A恰好没有滑离B板．已知A、B之间的动摩擦因数μ＝0.40，取g＝10 m/s².求：

图9

(1)A、B相对运动时的加速度a_A和a_B的大小与方向；

(2)A相对地面速度为零时，B相对地面运动已发生的位移大小x；

(3)木板B的长度l.

审题与关联

解析　(1)A、B分别受到大小为μmg的摩擦力作用，根据牛顿第二定律

对A有μmg＝ma_A

则a_A＝μg＝4.0 m/s²

方向水平向右

对B有μmg＝Ma_B

则a_B＝μmg/M＝1.0 m/s²

方向水平向左

(2)开始阶段A相对地面向左做匀减速运动，设到速度为零时所用时间为t₁，则v₀＝a_At₁，解得t₁＝v₀/a_A＝0.50 s

B相对地面向右做匀减速运动x＝v₀t₁－a_Bt＝0.875 m

(3)A先相对地面向左匀减速运动至速度为零，后相对地面向右做匀加速运动，加速度大小仍为a_A＝4.0 m/s²

B板向右一直做匀减速运动，加速度大小为a_B＝1.0 m/s²

当A、B速度相等时，A滑到B最左端，恰好没有滑离木板B，故木板B的长度为这个全过程中A、B间的相对位移．

在A相对地面速度为零时，B的速度

v_B＝v₀－a_Bt₁＝1.5 m/s

设由A速度为零至A、B速度相等所用时间为t₂，则

a_At₂＝v_B－a_Bt₂

解得t₂＝v_B/(a_A＋a_B)＝0.3 s

共同速度v＝a_At₂＝1.2 m/s

从开始到A、B速度相等的全过程，利用平均速度公式可知A向左运动的位移

x_A＝＝ m＝0.32 m

B向右运动的位移

x_B＝＝ m＝1.28 m

B板的长度l＝x_A＋x_B＝1.6 m

答案　(1)A的加速度大小为4.0 m/s²，方向水平向右　B的加速度大小为1.0 m/s²，方向水平向左　(2)0.875 m　(3)1.6 m

高考题组

1．模型特点：上、下叠放两个物体，并且两物体在摩擦力的相互作用下发生相对滑动．

13.“滑块—木板模型”问题的分析思路

2．建模指导

传送带模型问题包括水平传送带问题和倾斜传送带问题．

(1)水平传送带问题：求解的关键在于对物体所受的摩擦力进行正确的分析判断．判断摩擦力时要注意比较物体的运动速度与传送带的速度，也就是分析物体在运动位移x(对地)的过程中速度是否和传送带速度相等．物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻．

(2)倾斜传送带问题：求解的关键在于认真分析物体与传送带的相对运动情况，从而确定其是否受到滑动摩擦力作用．如果受到滑动摩擦力作用应进一步确定其大小和方向，然后根据物体的受力情况确定物体的运动情况．当物体速度与传送带速度相等时，物体所受的摩擦力有可能发生突变．

例4　如图8所示为某工厂的货物传送装置，倾斜运输带AB(与水平面成α＝37°)与一斜面BC(与水平面成θ＝30°)平滑连接，B点到C点的距离为L＝0.6 m，运输带运行速度恒为v₀＝5 m/s，A点到B点的距离为x＝4.5 m，现将一质量为m＝0.4 kg的小物体轻轻放于A点，物体恰好能到达最高点C点，已知物体与斜面间的动摩擦因数μ₁＝，求：(g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8，空气阻力不计)

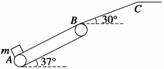
图8

(1)小物体运动到B点时的速度v的大小；

(2)小物体与运输带间的动摩擦因数μ；

(3)小物体从A点运动到C点所经历的时间t.

审题与关联

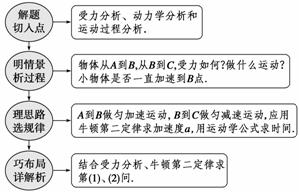
解析　(1)设小物体在斜面上的加速度为a₁，运动到B点的速度为v，由牛顿第二定律得

mgsin θ＋μ₁mgcos θ＝ma₁

由运动学公式知v²＝2a₁L，联立解得v＝3 m/s.

(2)因为v<v₀，所以小物体在运输带上一直做匀加速运动，设加速度为a₂，则由牛顿第二定律知

μmgcos α－mgsin α＝ma₂

又因为v²＝2a₂x，联立解得μ＝.

(3)小物体从A点运动到B点经历时间t₁＝，从B运动到C经历时间t₂＝

联立并代入数据得小物体从A点运动到C点所经历的时间t＝t₁＋t₂＝3.4 s.

答案　(1)3 m/s　(2)　(3)3.4 s

解答传送带问题应注意的事项

(1)水平传送带上物体的运动情况取决于物体的受力情况，即物体所受摩擦力的情况；倾斜传送带上物体的运动情况取决于所受摩擦力与重力沿斜面的分力情况．

(2)传送带上物体的运动情况可按下列思路判定：相对运动→摩擦力方向→加速度方向→速度变化情况→共速，并且明确摩擦力发生突变的时刻是v_物＝v_传．

(3)倾斜传送带问题，一定要比较斜面倾角与动摩擦因数的大小关系．

1．模型特征

一个物体以速度v₀(v₀≥0)在另一个匀速运动的物体上开始运动的力学系统可看做“传送带”模型，如图7(a)、(b)、(c)所示．

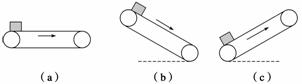
图7