
1、(08全国卷2)18. 如图,一很长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳两端各系一小球a和b.a球质量为m,静置于地面;b球质量为3m, 用手托住,高度为h,此时轻绳刚好拉紧.从静止开始释放b后,a可能达到的最大高度为
A.h B.1.5h C.2h D.2.5h
答案:B
解析:在b落地前,a、b组成的系统机械能守恒,且a、b两物体速度大小相等,根据机
械能守恒定律可知: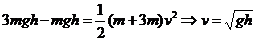 ,b球落地时,a球高度为h,之后a球向上做竖直上抛运动,过程中机械能守恒,
,b球落地时,a球高度为h,之后a球向上做竖直上抛运动,过程中机械能守恒,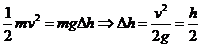 ,所以a可能达到的最大高度为1.5h,B项正确。
,所以a可能达到的最大高度为1.5h,B项正确。
28、(1)设物块的质量为m,其开始下落处的位置距BC的竖直高度为h,到达B点时的速度为v,小车圆弧轨道半径为R。由机械能守恒定律,有: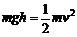 ①
①
根据牛顿第二定律,有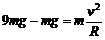 ② , 解得h=4R ③
② , 解得h=4R ③
即物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的4倍。
(2)设物块与BC间的滑动摩擦力的大小为F,物块滑到C点时与小车的共同速度为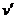 ,物块在小车上由B运动到C的过程中小车对地面的位移大小为s。依题意,小车的质量为3m,BC长度为10R。由滑动摩擦定律,有:
,物块在小车上由B运动到C的过程中小车对地面的位移大小为s。依题意,小车的质量为3m,BC长度为10R。由滑动摩擦定律,有: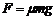 ④
④
由动量守恒定律,有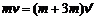 ⑤
⑤
对物块、小车分别应用动能定理,有: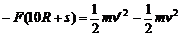 ⑥
⑥
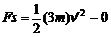 ⑦ ,解得
⑦ ,解得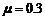 ⑧
⑧
2008
27、(1)滑块在圆盘上做圆周运动时,静摩擦力充当向心力,根据牛顿第二定律,
可得: 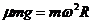 ① , 代入数据解得:
① , 代入数据解得: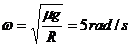 ②
②
(2)滑块在A点时的速度: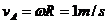 ③
③
从A到B的运动过程由动能定理: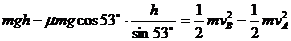 ④
④
在B点时的机械能: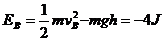 ⑤
⑤
(3)滑块在B点时的速度: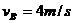 ⑥
⑥
滑块沿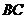 段向上运动时的加速度大小:
段向上运动时的加速度大小: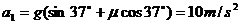 ⑦
⑦
返回时的加速度大小: 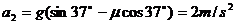 ⑧
⑧
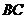 间的距离
间的距离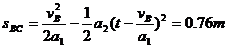 ⑨
⑨
26、(1)在G点,运动员和滑板一起做圆周运动,设向心加速度为an,速度为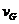 ,运动员受到重力Mg、滑板对运动员的支持力N的作用,则
,运动员受到重力Mg、滑板对运动员的支持力N的作用,则
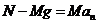 ① ,
① ,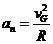 ②
②
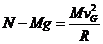 ③ ,
③ ,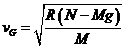 ④
④
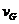 =6.5m/s ⑤
=6.5m/s ⑤
(2)设滑板。由A点静止下滑到BC赛道后速度为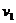 ,由机械能守恒定律有
,由机械能守恒定律有
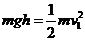 ⑥ ,
⑥ ,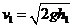 ⑦
⑦
运动员与滑板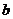 一起由A点静止下滑到BC赛道后,速度也为
一起由A点静止下滑到BC赛道后,速度也为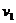 ,运动员由滑板b跳到滑板a,设蹬离滑板b时的水平速度为
,运动员由滑板b跳到滑板a,设蹬离滑板b时的水平速度为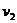 ,在空中飞行的水平位移为s,
,在空中飞行的水平位移为s,
则:s=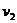 t2
⑧
t2
⑧
设起跳时滑板a与滑板b的水平距离为so,则:s0=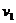 tl ⑨
tl ⑨
设滑板。在t2时间内的位移为s1,则
s1=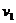 t2 ⑩ , s=s0+s1 ⑾ ,即
t2 ⑩ , s=s0+s1 ⑾ ,即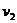 t2=
t2=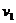 (t1+t2) ⑿
(t1+t2) ⑿
运动员落到滑板a后,与滑板a共同运动的速度为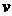 ,由动量守恒定律有
,由动量守恒定律有
m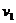 +M
+M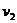 =(m+M)
=(m+M) 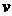 ⒀
⒀
由以上方程可解出: ⒁
⒁
代人数据,解得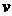 =6.9m/s ⒂
=6.9m/s ⒂
(3)设运动员离开滑板b后,滑板b的速度为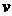 3,有
3,有
M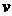 2+m
2+m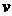 3=(M+m)
3=(M+m) 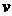 1 ⒃
1 ⒃
可算出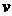 3=-3m/s,有:│
3=-3m/s,有:│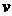 3│=3m/s<
3│=3m/s<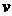 1=6m/s,b板将在两个平台之间来回运动,机械能不变。系统的机械能改变为:
1=6m/s,b板将在两个平台之间来回运动,机械能不变。系统的机械能改变为: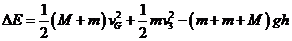 ⒄
⒄
△E=88.75J⒅
25、(1)设碰撞后的一瞬间,球B的速度为vB/,由于球B恰好与悬点O同一高度,根据动能定理: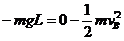 ① ,
① ,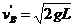 ②
②
(2)球A达到最高点时,只有水平方向速度,与球B发生弹性碰撞.设碰撞前的一瞬间,球A水平方向速度为vx.碰撞后的一瞬间,球A速度为vx/.球A、B系统碰撞过程中动量守恒和机械能守恒: ③
③
 ④
④
由②③④解得: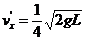 ⑤
⑤
及球A在碰撞前的一瞬间的速度大小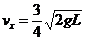 ⑥
⑥
(3)碰后球A作平抛运动.设从抛出到落地时间为t,平抛高度为y,则:
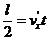 ⑦
,
⑦
,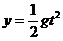 ⑧
,由⑤⑦⑧得:y=L
⑧
,由⑤⑦⑧得:y=L
以球A为研究对象,弹簧的弹性力所做的功为W,从静止位置运动到最高点:
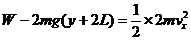 ⑨
⑨
由⑤⑥⑦得:W=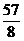 mgL ⑩
mgL ⑩
24、设构成铍“副射”的中性粒子的质量和速度分别为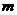 和
和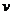 ,氢核的质量为
,氢核的质量为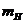 。构成铍“辐射”的中性粒子与氢核发生弹性正碰,碰后两粒子的速度分别为
。构成铍“辐射”的中性粒子与氢核发生弹性正碰,碰后两粒子的速度分别为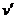 和
和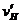 。由动量守恒与能量守恒定律得:
。由动量守恒与能量守恒定律得: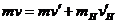 ① ,
① ,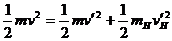 ②
②
解得: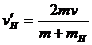 ③
③
同理,对于质量为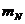 的氮核,其碰后速度为:
的氮核,其碰后速度为: ④
④
由③④式可得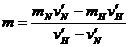 ⑤ ,根据题意可知:
⑤ ,根据题意可知: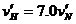 ⑥
⑥
将上式与题给数据代入⑤式得: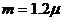 ⑦
⑦
23、解:设:小球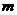 的摆线长度为
的摆线长度为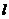
小球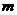 在下落过程中与
在下落过程中与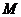 相碰之前满足机械能守恒:
相碰之前满足机械能守恒: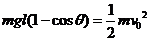 ①
①
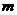 和
和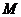 碰撞过程满足:
碰撞过程满足: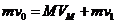 ②
②
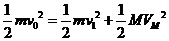 ③ , 联立
②③得:
③ , 联立
②③得: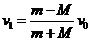 ④
④
说明小球被反弹,而后小球又以反弹速度和小球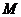 发生碰撞,满足:
发生碰撞,满足:
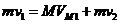 ⑤ ,
⑤ , 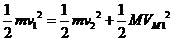 ⑥
⑥
解得: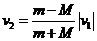 ⑦ , 整理得:
⑦ , 整理得: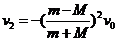 ⑧
⑧
所以: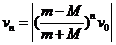 ⑨
⑨
而偏离方向为450的临界速度满足: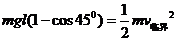 ⑩
⑩
联立① ⑨ ⑩代入数据解得,当n=2时,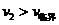
当n=3时,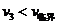 ,所以,最多碰撞3次
,所以,最多碰撞3次
22、从两小球碰撞后到它们再次相遇,小球A和B的速度大小保持不变,根据它们通过的路程,可知小球B和小球A在碰撞后的速度大小之比为4∶1。
设碰撞后小球A和B的速度分别为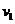 和
和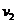 ,在碰撞过程中动量守恒,碰撞前后动能相等
,在碰撞过程中动量守恒,碰撞前后动能相等
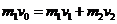 ,
, 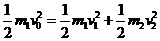
利用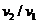 =4,可解出:
=4,可解出: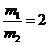
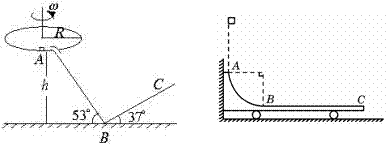
28、(2007天津)如图所示,水平光滑地面上停放着一辆小车,左侧靠在竖直墙壁上,小车的四分之一圆弧轨道AB是光滑的,在最低点B与水平轨道BC相切,BC的长度是圆弧半径的10倍,整个轨道处于同一竖直平面内。可视为质点的物块从A点正上方某处无初速度下落,恰好落入小车圆弧轨道滑动,然后沿水平轨道沿街至轨道末端C处恰好没有滑出。已知物块到达圆弧轨道最低点B时对轨道的压力是物块重力的9倍,小车的质量是物块的3倍,不考虑空气阻力和物块落入圆弧轨道时的能量损失。求
(1)物块开始下落的位置距水平轨道BC的竖直高度是圆弧半径的几倍;
(2)物块与水平轨道BC间的动摩擦因数μ。
27、(2007山东)如图所示,一水平圆盘绕过圆心的竖直轴转动.圆盘边缘有一质量m=1.0kg的小滑块。当圆盘转动的角速度达到某一数值时,滑块从圆盘边缘滑落,经光滑的过渡圆管进入轨道ABC。已知AB段斜面倾角为53°,BC段斜面倾角为37°,滑块与圆盘及斜面间的动摩擦因数均为μ=0.5。A点离B点所在水平面的高度h=1.2m。滑块在运动过程中始终未脱离轨道,不计在过渡圆管处和B点的机械能损失,最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8。
(1)若圆盘半径R=0.2m,当圆盘的角
速度多大时,滑块从圆盘上滑落?
(2)若取圆盘所在平面为零势能面,求
滑块到达B点时的机械能。
(3)从滑块到达B点时起,经0.6s正好通过C点,求BC之间的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com