
13.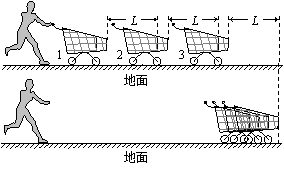 (2011年高考·重庆理综卷)如图所示,静置于水平地面的三辆手推车沿一直线排列,质量均为m,人在极短时间内给第一辆车一水平冲量使其运动,当车运动了距离L时与第二辆车相碰,两车以共同速度继续运动了距离L时与第三车相碰,三车以共同速度又运动了距离L时停止。车运动时受到的摩擦阻力恒为车所受重力的k倍,重力加速度为g,若车与车之间仅在碰撞时发生相互作用,碰撞时间很短,忽略空气阻力,求:
(2011年高考·重庆理综卷)如图所示,静置于水平地面的三辆手推车沿一直线排列,质量均为m,人在极短时间内给第一辆车一水平冲量使其运动,当车运动了距离L时与第二辆车相碰,两车以共同速度继续运动了距离L时与第三车相碰,三车以共同速度又运动了距离L时停止。车运动时受到的摩擦阻力恒为车所受重力的k倍,重力加速度为g,若车与车之间仅在碰撞时发生相互作用,碰撞时间很短,忽略空气阻力,求:
⑴整个过程中摩擦阻力所做的总功;
⑵人给第一 辆车水平冲量的大小;
辆车水平冲量的大小;
⑶第一次与第二次碰撞系统动能损失之比。
12.解析:设子弹初速度为v0,射入厚度为2d的钢板后,最终钢板和子弹的共同速度为V
由动量守恒得 (2m+m)V=mv0 ①
解得 V=v0
此过程中动能损失为 △E=mv02-×3m V2 ②
V2 ②
解得 △E=mv02
分成两块钢板后,设子弹穿过第一块钢板时两者的速度分别为v1和V 1,
1,
由动量守恒得 mv1+mV1=mv0  ③
③
因为子弹在钢板中受到的阻力为恒力, 射穿第一块钢板的动能损失为,
射穿第一块钢板的动能损失为,
由能量守恒得 mv12+mV12=mv02- ④
联立①②③④式,且考虑到v1必须大于V1,得 v1=(+)v0 ⑤
设子弹射入第二块钢板并留在其中后两者的共同速度为V2,
由动量守恒得 2mV2=mv1  ⑥
⑥
损失的动能为 △E′=mv12-×2mV22 ⑦
联立①②⑤⑥⑦式得△E′=(1+)× ⑧
因为子弹在钢板中受到的阻力为恒力,由⑧式keep,射入第二块钢板的深度x为
x=(1+)d ⑨
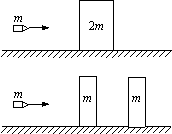
12.(2011年高考·全国大纲版理综卷)装甲车和战舰 采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击。通过对一下简化模型的计算可以粗略说明其原因。质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿。现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示。若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度。设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞。不计重力影响。
采用多层钢板比采用同样质量的单层钢板更能抵御穿甲弹的射击。通过对一下简化模型的计算可以粗略说明其原因。质量为2m、厚度为2d的钢板静止在水平光滑桌面上。质量为m的子弹以某一速度垂直射向该钢板,刚好能将钢板射穿。现把钢板分成厚度均为d、质量均为m的相同两块,间隔一段距离水平放置,如图所示。若子弹以相同的速度垂直射向第一块钢板,穿出后再射向第二块钢板,求子弹射入第二块钢板的深度。设子弹在钢板中受到的阻力为恒力,且两块钢板不会发生碰撞。不计重力影响。

11.解析:(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则mv12+mgL=mv02,则v1=m/s,
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则F+mg=m
联立解得F=2N,由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上。
(2)解除锁定后,设小球通过最高点时的速度为v2,此时滑块的速度为V。在上升过程中,因系统在水平方向上不受外力作用,水平方向的动量守恒。以水平向右的方向为正方向,有mv2+MV=0
在上升过程中,因只有重力做功,系统的机械能守恒,则mv22+MV2+mgL=mv02,联立解得v2=2m/s
(3)设小球击中滑块右侧轨道的位置点与小球起始点的距离为s1,滑块向左移动的距离为s2,任意时刻小球的水平速度大小为v3,滑块的速度大小为V/。由系统水平方向的动量守恒,得
mv3-MV′=0,两边同乘以△t,得mv3△t-MV′△t=0,故对任意时刻附近的微小间隔△t都成立,累积相加后,有ms1-Ms2=0,又s1+s2=2L,得s1=m
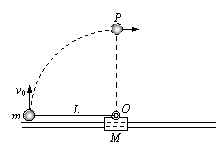
11.(2011年高考·安徽理综卷)如图所示,质量M=2kg 的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动。开始轻杆处于水平状态。现给小球一个竖直向上的初速度v0=4m/s,g取10m/s2。
的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动。开始轻杆处于水平状态。现给小球一个竖直向上的初速度v0=4m/s,g取10m/s2。
⑴若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向。
⑵若解除对滑块的锁定,试求小球通过最高点时的速度大小。
⑶在满足⑵的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。

10.解析:设某时刻MN和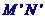 速度分别为v1、v2。
速度分别为v1、v2。
(1)MN和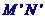 动量守恒:mv1-2mv2=0 求出:
动量守恒:mv1-2mv2=0 求出: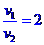 ①
①
(2)当MN和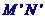 的加速度为零时,
的加速度为零时, 速度最大
速度最大
对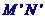 受力平衡:BIl=2mg ②,
受力平衡:BIl=2mg ②,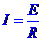 ③,
③,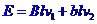 ④
④
由①②③④得: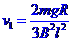 、
、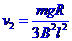
10.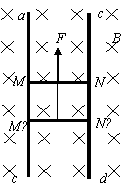 (2011年高考·海南理综卷)如图,ab和cd是两条竖直放置的长直光滑金属导轨,MN和M′N′是两根用细线连接的金属杆,其质量分别为m和2m。竖直向上的外力F作用在杆MN上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R,导轨间距为l。整个装置处在磁感应强度为B的匀强磁场中,磁场方向与导轨所在平面垂直。导轨电阻可忽略,重力加速度为g。在t=0时刻将细线烧断,保持F不变,金属杆和导轨始终接触良好。求
(2011年高考·海南理综卷)如图,ab和cd是两条竖直放置的长直光滑金属导轨,MN和M′N′是两根用细线连接的金属杆,其质量分别为m和2m。竖直向上的外力F作用在杆MN上,使两杆水平静止,并刚好与导轨接触;两杆的总电阻为R,导轨间距为l。整个装置处在磁感应强度为B的匀强磁场中,磁场方向与导轨所在平面垂直。导轨电阻可忽略,重力加速度为g。在t=0时刻将细线烧断,保持F不变,金属杆和导轨始终接触良好。求
(1)细线烧 断后,任意时刻两杆运动的速度之比;
断后,任意时刻两杆运动的速度之比;
(2)两杆分别达到的最大速度。
9.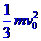 解析:设碰后A、B和C的共同速度的大小为v,由动量守恒得
解析:设碰后A、B和C的共同速度的大小为v,由动量守恒得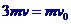 ①
①
设C离开弹簧时,A、B的速度大小为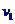 ,由动量守恒得
,由动量守恒得 ②
②
设弹簧的弹性势能为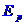 ,从细线断开到C与弹簧分开的过程中机械能守恒,有
,从细线断开到C与弹簧分开的过程中机械能守恒,有

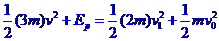 ③
③
由①②③式得弹簧所释放的势能为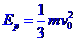 。
。
9.(2011年高考·全国卷新课标版)如图,A、B、C三个木块的质量均为m。置于光滑的水平面上,B、C之间有一轻质弹簧,弹簧的两端与木块接触而不固连 。将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体。现A以初速v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起。以后细线突然断开,弹簧伸展,从而
。将弹簧压紧到不能再压缩时用细线把B和C紧连,使弹簧不能伸展,以至于B、C可视为一个整体。现A以初速v0沿B、C的连线方向朝B运动,与B相碰并粘合在一起。以后细线突然断开,弹簧伸展,从而 使C与A、B分离。已知C离开弹簧后的速度恰为v0。求弹簧释放的势能。
使C与A、B分离。已知C离开弹簧后的速度恰为v0。求弹簧释放的势能。
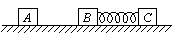

8.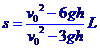 解析:(i)设木块和物体P共同速度为v,两物体从开始到第一次到达共同速度过程由动量和能量守恒得:
解析:(i)设木块和物体P共同速度为v,两物体从开始到第一次到达共同速度过程由动量和能量守恒得: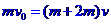 ① ;
① ;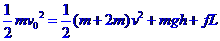 ②
②
由①②得: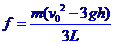 ③。
③。
(ii)木块返回与物体P 第二次达到共同速度与第一次相同(动量守恒)全过程能量守恒得:
第二次达到共同速度与第一次相同(动量守恒)全过程能量守恒得:
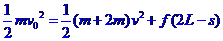 ④
④
由②③④得: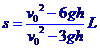 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com