
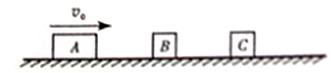
38.(2012 山东)(2)光滑水平轨道上有三个木块A、B、C,质量分别为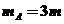 、
、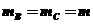 ,开始时B、C均静止,A以初速度向右运动,A与B相撞后分开,B又与C发生碰撞并粘在一起,此后A与B间的距离保持不变。求B与C碰撞前B的速度大小。
,开始时B、C均静止,A以初速度向右运动,A与B相撞后分开,B又与C发生碰撞并粘在一起,此后A与B间的距离保持不变。求B与C碰撞前B的速度大小。
[答案](1)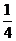 (2)
(2)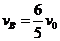
解析:(2)设A与B碰撞后,A的速度为,B与C碰撞前B的速度为,B与V碰撞后粘在一起的速度为,由动量守恒定律得
对A、B木块: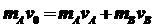 1
1
对B、C木块: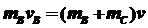 2
2
由A与B间的距离保持不变可知
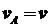 3
3
联立123式,代入数据得
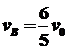 4
4
(2012 天津)9(1)质量为0.2kg的小球竖直向下以6m/s的速度落至水平地面,再以4m/s的速度反向弹回,取竖直向上为正方向,则小球与地面碰撞前后的动量变化为______kg·m/s。若小球与地面的作用时间为0,2s,则小球收到地面的平均作用力大小为______N(g=10m/s2)
29.(2012 福建)(2)如图,质量为M的小船在静止水面上以速率V0 向右匀速行驶,一质量为m的救生员站在船尾,相对小船静止。若救生员以相对水面速率v水平向左跃入水中,则救生员跃出后小船的速率为______。(填选项前的字母)
A. 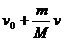 B.
B. 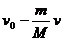
C.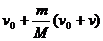 D.
D.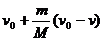

[考点]考查动量守恒定律的应用
[解析]人在跃出的过程中船人组成的系统水平方向动量守恒,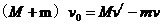 ,解得
,解得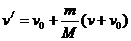 ,C项正确。
,C项正确。
[答案]C
24.(2012 北京)(20分)匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示,图中E0和d均为已知量。将带正电的质点A在O点由静止释放。A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放。当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相互作用视为静电作用。已知A的电荷量为Q,A和B的质量分别为m和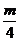 。不计重力。
。不计重力。
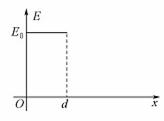
(1)求A在电场中的运动时间t;
(2)若B的电荷量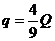 ,求两质点相互作用能的最大值Epm;
,求两质点相互作用能的最大值Epm;
(3)为使B离开电场后不改 变运动方向,求B所带电荷量的最大值qm。
变运动方向,求B所带电荷量的最大值qm。
解析:(1)A在电场中做匀加速直线运动位移为d,根据牛顿第二定律
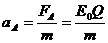 ①
①
根据位移公式得
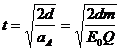
(2)设A、B分别离开电场后的速度为vA和vB,根据动能定理有
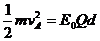 ②
②
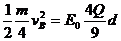 ③
③
由以上两式比较可知A、B分别离开电场后的速度为vA小于vB,所以B离开电场后与A间的静电斥力使B减速,使A加速,A、B系统的总动能减小,相互作用能增大,当A、B的速度相同为v时系统的总动能最小,相互作用能最大,在此过程中只有相互作用的静电斥力系统的能量和动量都守恒有
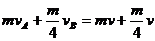 ④
④
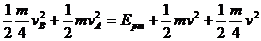 ⑤
⑤
连立②③④⑤四式解得
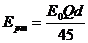
(3)A、B间距达到最小后静电斥力继续使B减速,使A加速,A、B系统的总动能增大,相互作用能减小,A、B间距达到无穷大时相互作用能为0。为使B离开电场后不改变运动方向,B的速度满足条件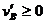 ⑥。根据系统的能量和动量都守恒有
⑥。根据系统的能量和动量都守恒有
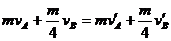 ⑦
⑦
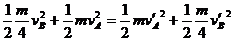 ⑧
⑧
③式中B的电量变为qB有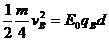 ⑨
⑨
连立②⑥⑦⑧⑨五式解得
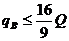 ,所以B所带电荷量的最大值
,所以B所带电荷量的最大值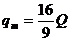
36.(2012 广东)(18分)
图18(a)所示的装置中,小物块A、B质量均为m,水平面上PQ段长为l,与物块间的动摩擦因数为μ,其余段光滑。初始时,挡板上的轻质弹簧处于原长;长为r的连杆位于图中虚线位置;A紧靠滑杆(A、B间距大于2r)。随后,连杆以角速度ω匀速转动,带动滑杆作水平运动,滑杆的速度-时间图像如图18(b)所示。A在滑杆推动下运动,并在脱离滑杆后与静止的B发生完全非弹性碰撞。
(1)求A脱离滑杆时的速度uo,及A与B碰撞过程的机械能损失ΔE。
(2)如果AB不能与弹簧相碰,设AB从P点到运动停止所用的时间为t1,求ω得取值范围,及t1与ω的关系式。
(3)如果AB能与弹簧相碰,但不能返回道P点左侧,设每次压缩弹簧过程中弹簧的最大弹性势能为Ep,求ω的取值范围,及Ep与ω的关系式(弹簧始终在弹性限度内)。
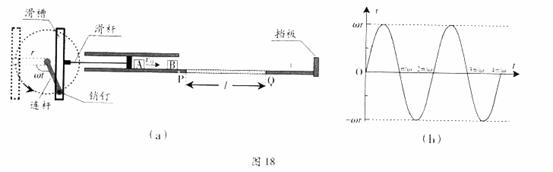
[考点]力学综合(牛顿运动定律、动量守恒、能量转换与守恒定律)
[答案](1)uo=ωr 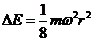
(2)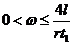
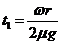
(3)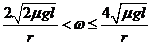
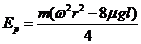
[解析](1)由题知,A脱离滑杆时的速度uo=ωr
设A、B碰后的速度为v1,由动量守恒定律
m uo=2m v1
A与B碰撞过程损失的机械能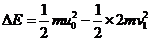
解得 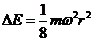
(2)AB不能与弹簧相碰,设AB在PQ上运动的加速度大小为a,由牛顿第二定律及运动学规律
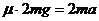 v1=at1
v1=at1
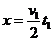
由题知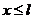
联立解得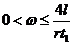
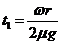
(3)AB能与弹簧相碰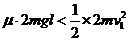
不能返回道P点左侧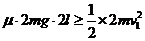
解得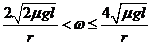
AB在的Q点速度为v2,AB碰后到达Q点过程,由动能定理
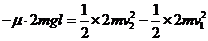
AB与弹簧接触到压缩最短过程,由能量守恒
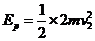
解得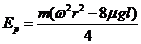
17.A [解题思路]带电粒子在匀强磁场中做匀速圆周运动,其半径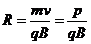 ,已知两粒子动量相等,若
,已知两粒子动量相等,若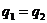 ,则它们的圆周运动半径一定相等,选项A正确;若
,则它们的圆周运动半径一定相等,选项A正确;若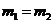 ,不能确定两粒子电量关系,不能确定半径是否相等,选项B错;由周期公式
,不能确定两粒子电量关系,不能确定半径是否相等,选项B错;由周期公式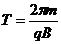 ,仅由电量或质量关系,无法确定两粒子做圆周运动的周期是否相等,选项C、D错。
,仅由电量或质量关系,无法确定两粒子做圆周运动的周期是否相等,选项C、D错。
17.(2012 大纲卷)分别为m1和m2、电荷量分别为q1和q2的两粒子在同一匀强磁场中做匀速圆周运动,已知两粒子的动量大小相等。下列说法正确的是
A.若q1=q2,则它们作圆周运动的半径一定相等
B.若m1=m2,则它们作圆周运动的周期一定相等
C. 若q1≠q2,则它们作圆周运动的半径一定不相等
D. 若m1≠m2,则它们作圆周运动的周期一定不相等
21.AD 解题思路] 两球在碰撞前后,水平方向不受外力,故水平两球组成的系统动量守恒,由动量守恒定律有: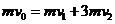 ;又两球碰撞是弹性的,故机械能守恒,即:
;又两球碰撞是弹性的,故机械能守恒,即: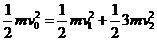 ,解两式得:
,解两式得: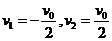 ,可见第一次碰撞后的瞬间,两球的速度大小相等,选项A正确;因两球质量不相等,故两球碰后的动量大小不相等,选项B错;两球碰后上摆过程,机械能守恒,故上升的最大高度相等,另摆长相等,故两球碰后的最大摆角相同,选项C错;由单摆的周期公式
,可见第一次碰撞后的瞬间,两球的速度大小相等,选项A正确;因两球质量不相等,故两球碰后的动量大小不相等,选项B错;两球碰后上摆过程,机械能守恒,故上升的最大高度相等,另摆长相等,故两球碰后的最大摆角相同,选项C错;由单摆的周期公式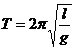 ,可知,两球摆动周期相同,故经半个周期后,两球在平衡位置处发生第二次碰撞,选项D正确。
,可知,两球摆动周期相同,故经半个周期后,两球在平衡位置处发生第二次碰撞,选项D正确。
21.(2012 大纲卷)如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触,现将摆球a向左边拉开一小角度后释放,若两球的碰撞是弹性的,下列判断正确的是
A.第一次碰撞后的瞬间,两球的速度大小相等
B.第一次碰撞后的瞬间,两球的动量大小相等
C.第一次碰撞后,两球的最大摆角不相同
D.发生第二次碰撞时,两球在各自的平衡位置

35.(2012新课标)(2)(9分)如图 ,小球a、b用等长细线悬挂于同一固定点O。让球a静止下垂,将球b向右拉起,使细线水平。从静止释放球b,两球碰后粘在一起向左摆动,此后细线与竖直方向之间的最大偏角为60°。忽略空气阻力,求
,小球a、b用等长细线悬挂于同一固定点O。让球a静止下垂,将球b向右拉起,使细线水平。从静止释放球b,两球碰后粘在一起向左摆动,此后细线与竖直方向之间的最大偏角为60°。忽略空气阻力,求
(i) 两球a、b的质量之比;
两球a、b的质量之比;
(ii)两球在碰撞过程中损失的机械能与球b在碰前的最大动能之比。


(2)[考点]动量守恒、能量守恒综合
解:(i)设球b的质量为m2,细线长为L,球b下落至最低点,但未与球a相碰时的速度为v,由机械能守恒定律得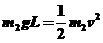 ①
①
式中g是重力加速度的大小。设球a的质量为m1;在两球碰后的瞬间,两球共同速度为v′,以向左为正。有动量守恒定律得 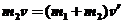 ②
②
设两球共同向左运动到最高处,细线与竖直方向的夹角为θ,由机械能守恒定律得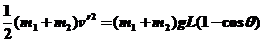 ③
③
联立①②③式得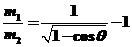
代入数据得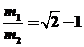
(ii)两球在碰撞过程中的机械能损失是 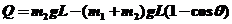
联立①⑥式,Q与碰前球b的最大动能Ek(Ek=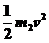 )之比为
)之比为
 ⑦
⑦
联立⑤⑦式,并代入题给数据得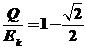 ⑧
⑧
13.解析:(1)设运动过程中摩擦阻力做的总功为W,则
 W=-kmgL-2kmgL-3kmgL=-6kmgL
W=-kmgL-2kmgL-3kmgL=-6kmgL
(2)设第一车初速度为u0,第一次碰前速度为v1,碰后共同速度为u1; 第二次碰前速度为v2,碰后共同速度为u2;人给第一车的水平冲量大小为I。
第二次碰前速度为v2,碰后共同速度为u2;人给第一车的水平冲量大小为I。
由: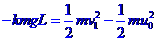 ,
,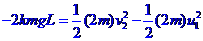 ,
,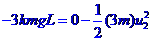
mv1=2mu1,2mv2=3mu2,得:I=mu0-0=2m
(3)设两次碰撞中系统动能损失分别为 △Ek1和△Ek2,由△Ek1=kmgL,△Ek2=kmgL[来源:]
△Ek1和△Ek2,由△Ek1=kmgL,△Ek2=kmgL[来源:]
得:△Ek1/△Ek2=13/3。
(2012上海)22A.A、B两物体在光滑水平地面上沿一直线相向而行,A质量为5kg,速度大小为10m/s,B质量为2kg,速度大小为5m/s,它们的总动量大小为_________kgm/s;两者相碰后,A沿原方向运动,速度大小为4m/s,则B的速度大小为_________m/s。40,10,
22A.[考点]本题考查动量守恒定律
[解析]设物体A运动的方向为正方向,则碰前的总动量大小为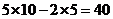 kg·m/s,碰撞前后动量守恒,则有
kg·m/s,碰撞前后动量守恒,则有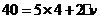 ,故碰后B的速度大小为
,故碰后B的速度大小为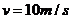
[答案]40,10
[误区警示]在应用动量守恒定律解答题目时,首先要规定正方向,然后把相关的物理量代入公式进行计算,若出现符号,需要说明符号的物理意义。该类型的题目容易出错的原因就在于正方向的规定。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com