3．两分力大小相等，夹角为120°时，可得F_合＝F.

例2　如图9所示是剪式千斤顶，当摇动把手时，螺纹轴就能迫使千斤顶的两臂靠拢，从而将汽车顶起．当车轮刚被顶起时汽车对千斤顶的压力为1.0×10⁵ N，此时千斤顶两臂间的夹角为120°，则下列判断正确的是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

图9

A．此时两臂受到的压力大小均为5.0×10⁴ N

B．此时千斤顶对汽车的支持力为2.0×10⁵ N

C．若继续摇动把手，将汽车顶起，两臂受到的压力将增大

D．若继续摇动把手，将汽车顶起，两臂受到的压力将减小

解析　把压力分解，得到此时两臂受到的压力大小均为1.0×10⁵ N，由牛顿第三定律，千斤顶对汽车的支持力为1.0×10⁵ N，若继续摇动把手，两臂间的夹角减小，而合力不变，故两分力减小，即两臂受到的压力减小．

答案　D

突破训练2　小娟、小明两人共提一桶水匀速前行，如图10所示，已知两人手臂上的拉力大小相等且为F，两人手臂间的夹角为θ，水和水桶的总重力为G，则下列说法中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　 (　)

图10

A．当θ为120°时，F＝G

B．不管θ为何值，F＝

C．当θ＝0°时，F＝

D．θ越大，F越小

答案　AC

解析　由力的合成可知，两分力与合力大小相等时，θ＝120°，F_合＝F_分＝G；θ＝0°，

F_分＝F_合＝，故A、C对，B错．θ越大，在合力一定时，分力越大，故D错．

考点三　力分解的两种常用方法

2．两分力大小相等，即F₁＝F₂＝F时(如图8所示)：

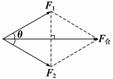
图8

F_合＝2Fcos .

1．两分力F₁、F₂互相垂直时(如图7所示)：

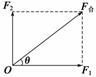
图7

F_合＝，tan θ＝.

2．重要结论

(1)二个分力一定时，夹角θ越大，合力越小．

(2)合力一定，二等大分力的夹角越大，二分力越大．

(3)合力可以大于分力，等于分力，也可以小于分力．

例1　一物体受到三个共面共点力F₁、F₂、F₃的作用，三力的矢量关系如图5所示(小方格边长相等)，则下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

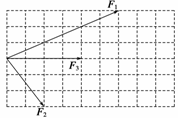
图5

A．三力的合力有最大值F₁＋F₂＋F₃，方向不确定

B．三力的合力有惟一值3F₃，方向与F₃同向

C．三力的合力有惟一值2F₃，方向与F₃同向

D．由题给条件无法求出合力大小

解析　根据三力的图示，知F₁、F₂在竖直方向分力的大小均为3个单位，方向相反，在水平方向的分力分别为6个单位和2个单位，方向与F₃方向相同．根据正交分解法求合力的思想知，3个力的合力为12个单位，与F₃的方向相同，大小是F₃的3倍，即F_合＝3F₃.选项B正确．

答案　B

突破训练1　如图6所示，一根不可伸长的轻绳穿过轻滑轮，两端系在高度相等的A、B两点，滑轮下挂一物体，不计轻绳和轻滑轮之间的摩擦．保持A固定不动，让B缓慢向右移动，则下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

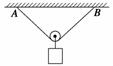
图6

A．随着B向右缓慢移动，绳子的张力减小

B．随着B向右缓慢移动，绳子的张力不变

C．随着B向右缓慢移动，滑轮受绳AB的合力变大

D．随着B向右缓慢移动，滑轮受绳AB的合力不变

答案　D

解析　动滑轮在不计摩擦的情况下，两侧绳子拉力大小相等，平衡后，两侧绳子的拉力关于竖直方向对称．保持A固定不动，让B缓慢向右移动，则两侧绳子的夹角增大，绳上的张力增大，由于物体的重力不变，故绳AB的合力不变．本题应选D.

考点二　几种特殊情况下的力的合成问题

1．共点力合成的方法

(1)作图法

(2)计算法：根据平行四边形定则作出示意图，然后利用解三角形的方法求出合力，是解题的常用方法．

5．力的分解

(1)概念：求一个力的分力的过程．

(2)遵循的原则：平行四边形定则或三角形定则．

(3)分解的方法

①按力产生的实际效果进行分解．

②正交分解法．

考点一　共点力的合成

4．矢量和标量

(1)矢量：既有大小又有方向的量．相加时遵循平行四边形定则．

(2)标量：只有大小没有方向的量．求和时按算术法则相加．

3．力的合成的运算法则

(1)平行四边形定则：求两个互成角度的共点力F₁、F₂的合力，可以用表示F₁、F₂的有向线段为邻边作平行四边形，平行四边形的对角线就表示合力的大小和方向，如图4甲所示．

(2)三角形定则：求两个互成角度的共点力F₁、F₂的合力，可以把表示F₁、F₂的线段首尾顺次相接地画出，把F₁、F₂的另外两端连接起来，则此连线就表示合力的大小和方向，如图乙所示．

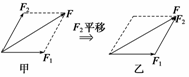
图4

2．共点力：作用在物体上的力的作用线或作用线的反向延长线交于一点的力．

1．合力与分力

(1)定义：如果一个力的作用效果跟几个力共同作用的效果相同，这一个力就叫那几个力的合力，那几个力就叫这个力的分力．

(2)逻辑关系：合力和分力是一种等效替代关系．