3．一件行李重为G，被绳OA和OB吊在空中，OA绳和OB绳的拉力分别为F₁、F₂，如图1所示，则　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

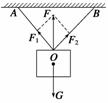
图1

A．F₁、F₂的合力是G

B．F₁、F₂的合力是F

C．行李对绳OA的拉力方向与F₁方向相反，大小相等

D．行李受到重力G、OA绳拉力F₁、OB绳拉力F₂，还有F共四个力

答案　BC

解析　合力与分力具有等效替代的关系．所谓等效是指力F的作用效果与其分力F₁、F₂共同作用产生的效果相同．F₁和F₂的合力的作用效果是把行李提起来，而G的作用效果是使行李下落，另外产生的原因(即性质)也不相同，故A错误；F₁和F₂的作用效果和F的作用效果相同，故B正确；行李对绳OA的拉力与拉行李的力F₁是相互作用力，等大反向，不是一个力，故C正确；合力F是为研究问题方便而假想出来的力，实际上不存在，应与实际受力区别开来，故D错误．

2．下列关于合力的叙述中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．合力是原来几个力的等效替代，合力的作用效果与分力的共同作用效果相同

B．两个力夹角为θ(0≤θ≤π)，它们的合力随θ增大而增大

C．合力的大小总不会比分力的代数和大

D．不是同时作用在同一物体上的力也能进行力的合成的运算

答案　AC

解析　力的合成的基本出发点是力的等效替代．合力是所有分力的一种等效力，它们之间是等效替代关系．合力和作用在物体上各分力间的关系，在效果上是和各分力的共同作用等效，而不是与一个分力等效．只有同时作用在同一物体上的力才能进行力的合成的运算．就合力与诸分力中的一个分力的大小相比较，则合力的大小可以大于、等于或小于该分力的大小，这是因为力是矢量．力的合成遵循平行四边形定则，合力的大小不仅跟分力的大小有关，而且跟分力的方向有关．根据力的平行四边形定则和数学知识可知，两个分力间夹角为θ(0≤θ≤π)，它们的合力随θ增大而减小．当θ＝0°时，合力最大，为两分力的代数和；当θ＝180°时，合力最小，等于两分力的代数差．所以合力的大小总不会比分力的代数和大．

1．三个共点力大小分别是F₁、F₂、F₃，关于它们合力F的大小，下列说法中正确的是(　)

A．F大小的取值范围一定是0≤F≤F₁＋F₂＋F₃

B．F至少比F₁、F₂、F₃中的某一个大

C．若F₁∶F₂∶F₃＝3∶6∶8，只要适当调整它们之间的夹角，一定能使合力为零

D．若F₁∶F₂∶F₃＝3∶6∶2，只要适当调整它们之间的夹角，一定能使合力为零

答案　C

解析　三个大小分别是F₁、F₂、F₃的共点力合成后的最大值一定等于F₁＋F₂＋F₃，但最小值不一定等于零，只有当某一个力的大小在另外两个力的大小的和与差之间时，这三个力的合力才可能为零，A、B、D错误，C正确．

4．如图16所示，重力为G的小球用轻绳悬于O点，用力F拉住小球，使轻绳保持偏离竖直方向60°角且不变，当F与竖直方向的夹角为θ时F最小，则θ、F的值分别为(　)

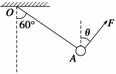
图16

A．0°，G

B．30°，G

C．60°，G

D．90°，G

答案　B

解析　分解小球重力．沿绳OA的分力方向确定，另一方向不确定，但由三角形定则可看出，另一分力F′的大小与θ角的大小有关．由数学知识可知，当F′的方向与绳OA垂直时F′最小，力F最小．所以θ＝30°，F_min＝Gcos 30°＝G，故B正确．

(限时：30分钟)

►题组1　对合力与分力的关系的理解

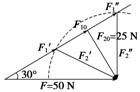
3．已知两个共点力的合力为50 N，分力F₁的方向与合力F的方向成30°角，分力F₂的大小为30 N．则　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．F₁的大小是唯一的　 　　　　　　　　　　　　 B．F₂的方向是唯一的

C．F₂有两个可能的方向　 　　　　　　　　　　　 D．F₂可取任意方向

答案　C

解析　由F₁、F₂和F的矢量三角形图可以看出：

当F₂＝F₂₀＝25 N时，F₁的大小才是唯一的，F₂的方向才是唯一的．因F₂＝30 N>F₂₀＝25 N，所以F₁的大小有两个，即F₁′和F₁″，F₂的方向有两个，即F₂′的方向和F₂″的方向，故选项A、B、D错误，选项C正确．

2．(2012·山东理综·17)如图15所示，两相同轻质硬杆OO₁、OO₂可绕其两端垂直纸面的水平轴O、O₁、O₂转动，在O点悬挂一重物M，将两相同木块m紧压在竖直挡板上，此时整个系统保持静止．F_f表示木块与挡板间摩擦力的大小，F_N表示木块与挡板间正压力的大小．若挡板间的距离稍许增大后，系统仍静止且O₁、O₂始终等高，则(　)

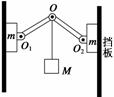
图15

A．F_f变小　 　　　　　　　　　　　 B．F_f不变

C．F_N变小　 　　　　　　　　　　　　　　 D．F_N变大

答案　BD

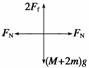解析　选重物M及两个木块m组成的系统为研究对象，系统受力情况

如图甲所示，根据平衡条件有2F_f＝(M＋2m)g，即F_f＝，与

两挡板间距离无关，故挡板间距离稍许增大后，F_f不变，所以选项A　　　　　　　 　 甲

错误，选项B正确；如图乙所示，将绳的张力F_T沿OO₁、OO₂两个方向分解为F₁、F₂，则F₁＝F₂＝，当挡板间距离稍许增大后，F_T不变，θ变大，cos θ变小，故F₁变大；选左边木块m为研究对象，其受力情况如图丙所示，根据平衡条件得F_N＝F₁sin θ，当两挡板间距离稍许增大后，F₁变大，θ变大，sin θ变大，因此F_N变大，故选项C错误，选项D正确．

乙　　　　　丙

模拟题组

1．(2013·重庆理综·1)如图14所示，某人静躺在椅子上，椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G，则椅子各部分对他的作用力的合力大小为　　　　　 (　)

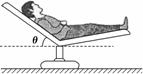
图14

A．G　 　　　　 B．Gsin θ　 　　　　　 C．Gcos θ　 　　　　 D．Gtan θ

答案　A

解析　椅子各部分对人的作用力的合力与重力G是平衡力．因此选项A正确．

6．实际问题模型化后的合成与分解

把力按实际效果分解的一般思路：

例5　如图13所示，两滑块放在光滑的水平面上，中间用一细线相连，轻杆OA、OB搁在滑块上，且可绕铰链O自由转动，两杆长度相等，夹角为θ，当竖直向下的力F作用在铰链上时，滑块间细线的张力为多大？

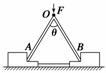
图13

解析　把竖直向下的力F沿两杆OA、OB方向分解，如图甲所示，可求出作用于滑块上斜向下的力为：F₁＝F₂＝

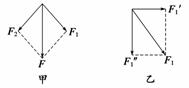
斜向下的压力F₁产生两个效果：竖直向下压滑块的力F₁″和沿水平方向推滑块的力F₁′，因此，将F₁沿竖直方向和水平方向分解，如图乙所示，考虑到滑块不受摩擦力，细线上的张力等于F₁在水平方向上的分力F₁′，即：

F₁′＝F₁cos ＝F₁sin

解得：F₁′＝tan

答案　tan

高考题组

2．正交分解法

(1)定义：将已知力按互相垂直的两个方向进行分解的方法．

(2)建立坐标轴的原则：以少分解力和容易分解力为原则(即尽量多的力在坐标轴上)．

例3　如图11所示，质量为M的正方形空木箱放置在粗糙水平面上，沿空木箱对角线有一光滑细轨道，轨道与水平方向间的夹角为45°.轨道上有一质量为m的物体沿轨道自由下滑，木箱始终静止在水平面上，求物体下滑的过程中，

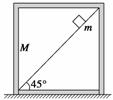
图11

(1)轨道对物体的弹力大小；

(2)地面对木箱的摩擦力的大小和方向．

解析　(1)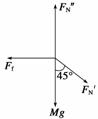以物体为研究对象，垂直轨道方向有F_N＝mgcos 45°

解得轨道对物体的弹力大小为

F_N＝mg

(2)以木箱为研究对象，受力如图所示．

由牛顿第三定律有F_N′＝F_N

在水平方向上有F_f＝F_N′sin 45°

解得F_f＝mg，方向向左．

答案　(1)mg　(2)mg，方向向左

例4　重为G₁＝8 N的砝码悬挂在轻绳PA和PB的结点上．PA偏离竖直方向37°角，PB在水平方向，且连在重力为G₂＝100 N的木块上，木块静止于倾角为θ＝37°的斜面上，如图12所示．试求：木块与斜面间的摩擦力大小和木块所受斜面的弹力大小．

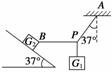
图12

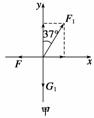
解析　对P点进行受力分析，建立如图甲所示的坐标系．

由水平方向和竖直方向列方程得：

F＝F₁sin 37°，G₁＝F₁cos 37°

联立解得F＝G₁tan 37°＝8× N＝6 N

对G₂进行受力分析建立如图乙所示的坐标系．

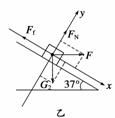
平行斜面方向上，Fcos θ＋G₂sin θ＝F_f

解得摩擦力F_f＝6×0.8 N＋100×0.6 N＝64.8 N

垂直斜面方向上，Fsin θ＋F_N＝G₂cos θ

解得弹力F_N＝100×0.8 N－6×0.6 N＝76.4 N

答案　64.8 N　76.4 N

　　　　　　　　　　　　　　　　　　　 力的合成法与分解方法的选择

力的效果分解法、正交分解法、合成法都是常见的解题方法，一般情况下，物体只受三个力的情形下，力的效果分解法、合成法解题较为简单，在三角形中找几何关系，利用几何关系或三角形相似求解；而物体受三个以上力的情况多用正交分解法，但也要视题目具体情况而定．

1．按力的效果进行分解：

(1)根据力的实际作用效果确定两个实际分力的方向；

(2)再根据两个实际分力的方向画出平行四边形；

(3)最后由平行四边形和数学知识求出两分力的大小．