
3. 抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率
A.大于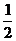 B.等于
B.等于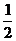 C.小于
C.小于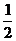 D.不能确定
D.不能确定
2.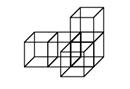 右图使用五个相同的立方体搭成的几何体,
右图使用五个相同的立方体搭成的几何体, 其主视图是
其主视图是

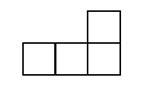
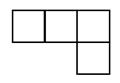
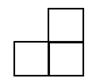
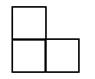
A B C
 D (第2题)
D (第2题)
一、选择题
1. 2-1等于
A.2 B.-2 C.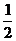 D.-
D.-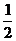
28.(本题12分)已知矩形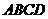 的一条边
的一条边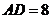 ,将矩形
,将矩形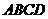 折叠,使得顶点
折叠,使得顶点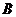 落在
落在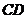 边上的
边上的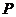 点处。
点处。
(1)如图1,已知折痕与边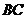 交于点
交于点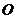 ,连接
,连接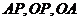 .
.
①求证: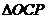 ∽
∽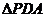 ;
;
②若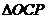 与
与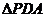 的面积比为1:4,求边
的面积比为1:4,求边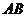 的长;
的长;
(2)若图1中的点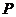 恰巧是
恰巧是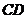 边的中点,求
边的中点,求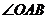 的度数;
的度数;
(3)如图2,在(1)条件下,擦去折痕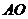 、线段
、线段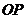 ,连结
,连结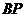 。动点
。动点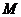 在线段
在线段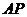 上(点
上(点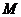 与点
与点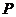 、
、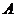 不重合),动点
不重合),动点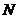 在线段
在线段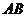 的延长线上,且
的延长线上,且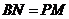 ,连结
,连结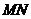 交
交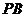 于点
于点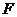 ,作
,作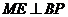 于点
于点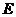 。试问当点
。试问当点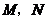 在移动过程中,线段
在移动过程中,线段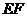 的长度是否发生变化?若变化,说明理由;若不变,求线段
的长度是否发生变化?若变化,说明理由;若不变,求线段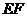 的长度。
的长度。






27.(本题12分)某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装,专卖店又缺少资金。“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)。已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量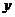 (件)与销售价
(件)与销售价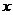 (元/件)之间的关系可用图中的一条折线(实线)来表示。该店支付员工的工资为每人每天82元,每天还应该支付其它费用为106元(不包含债务)。
(元/件)之间的关系可用图中的一条折线(实线)来表示。该店支付员工的工资为每人每天82元,每天还应该支付其它费用为106元(不包含债务)。
(1)求日销售量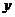 (件)与销售价
(件)与销售价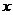 (元/件)之间的函数关系式;
(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收入=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?

26.(本题10分)对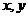 定义一种新运算
定义一种新运算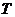 ,规定:
,规定: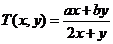 (其中
(其中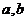 均为非零常数),这里等式右边是通常的四则运算,例如:
均为非零常数),这里等式右边是通常的四则运算,例如: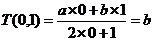 。
。
(1)已知
①求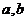 的值;
的值;
②若关于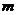 的不等式组
的不等式组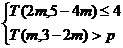 恰好有3个整数解,求实数
恰好有3个整数解,求实数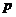 的取值范围;
的取值范围;
(2)若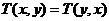 对任意实数
对任意实数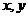 都成立(这里
都成立(这里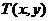 ,
, 都有意义),则
都有意义),则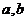 应满足怎样的关系式?
应满足怎样的关系式?
25.(本题10分)如图,圆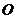 与
与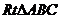 的斜边
的斜边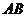 相切于点
相切于点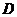 ,与直角边
,与直角边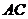 相交于
相交于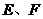 两点,连结
两点,连结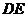 ,已知
,已知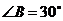 ,圆
,圆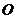 的半径为12,弧
的半径为12,弧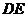 的长度为
的长度为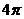 。
。
(1) 求证:
求证: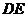 ∥
∥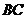 ;
;
(2)若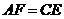 ,求线段
,求线段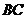 的长度。
的长度。
24.(本题10分)某漆器厂接到制作480件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务,原来每天制作多少件?
23.(本题10分)如图,已知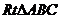 中,
中,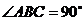 ,先把
,先把 绕点
绕点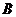 顺时针旋转
顺时针旋转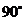 至
至 后,再把
后,再把 沿射线
沿射线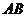 平移至
平移至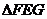 ,
,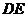 、
、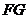 相交于点
相交于点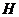 。
。
(1)判断线段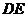 、
、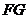 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)连结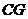 ,求证:四边形
,求证:四边形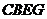 是正方形。
是正方形。

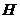
22.(本题8分)商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同。
(1)若他去买一瓶饮料,则他买到奶汁的概率是_________;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶油的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com