
26.解:(1)A(-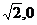 )
)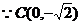 ,
,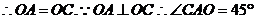 .(3分)
.(3分)
(2)如图1,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线α旋转到α1恰好与⊙B1第一次相切于点P,⊙B1与x轴相切于点N,连接B1O,B1N,则MN=t,OB1=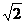 ,
,
 B1N⊥AN ∴MN=3 即t=3…………………………………………………………5分
B1N⊥AN ∴MN=3 即t=3…………………………………………………………5分
连接B1A,B1P, 则B1P⊥AP, B1P=B1N ∴∠PAB1=∠NAB1
∵OA=OB1=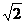
∴∠AB1O=∠NAB1
∴∠PAB1=∠AB1O
∴PA∥B1O
在Rt△NOB1中, ∠B1ON=45°,
∴∠PAN=45°,∴∠1=90°
∴直线AC绕点A平均每秒30°.……………9分
(3)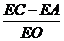 的值不变,等于
的值不变,等于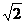 ,……………………………………………………11分
,……………………………………………………11分
 如图2在CE上截取CK=EA,连接OK,
如图2在CE上截取CK=EA,连接OK,
∵∠OAE=∠OCK, OA=OC ∴△OAE≌△OCK
∴OE=OK,∠EOA=∠KOC ∴∠EOK=∠AOC=90°
∴EK=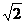 EO
EO
∴ ………………………………14分
………………………………14分
25. 解:(1)A地位置如图所示.使点A满足AB=60千米,AC=90千米,(或AB:AC=2:3);………………………………2分
解:(1)A地位置如图所示.使点A满足AB=60千米,AC=90千米,(或AB:AC=2:3);………………………………2分
(2)乙车的速度150÷2=75千米/时,
90÷75=1.2,
 ∴M(1.2,0)……………………………………4分
∴M(1.2,0)……………………………………4分
所以点M表示乙车1.2小时到达A地;………5分
(3)甲车的函数图象如图所示:………………7分
当0≤x≤1时,y1=-60x+60;……………………8分
当1<x≤2.5时,y1=60x-60;…………………9分
(4)由题意得甲车与指挥中心的通话时间为:
 得
得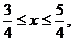 ………………11分
………………11分
乙车与指挥中心的通话时间: 得
得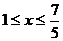 ,……………………12分
,……………………12分
∴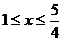 .……………………………………………………………………………13分
.……………………………………………………………………………13分
∴两车同时与指挥中心通话的时间为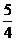 -1=
-1= 小时.………………………………14分
小时.………………………………14分
24.解:(1) y=-x2+nx;…………………………………………………………………2分
(2)∵在Rt△OMN中tan∠NOP=2,而tan∠NOP=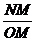 ,
,
∵AD⊥x轴,A(4,4),D(4,6),∴OM=4,MN=8,N(4,8),……………3分
∴将点N的坐标代入y=-x2+nx,得n=6,即y=-x2+6x,………………………4分
∵Q(m,2m-5)在抛物线上,
∴2m-5=-m2+6m,即m2-4m-5=0,………………………………………………5分
∴m=5或m=-1,………………………………………………………………………7分
∵点Q在第一象限,∴Q(5,5),………………………………………………………8分
∵直线MN为x=4,
∴点Q关于直线MN对称的点的坐标为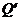 (3,5);…………………………………9分
(3,5);…………………………………9分
(3)5≤n≤7.……………………………………………………………………………11分
23. 解:(1)a=
解:(1)a= ;……………………………………1分
;……………………………………1分
b=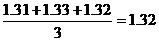 ;……………………2分
;……………………2分
β=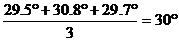 ;………………3分
;………………3分
(2)过C作CE⊥AB于E,则四边形EBDC是矩形,……………………………………………………4分
∴CE=BD=aBE=CD=b,……………………………5分
在Rt△AEC中,∵β=30°,a=15.81,
∴AE=CEtan30°=15.81× ≈9.128(米),……………………………………………8分
≈9.128(米),……………………………………………8分
则AB=AE+EB=9.128+1.32=10.448≈10.45(米).………………………………………9分
答:风筝的高度AB为10.45米.………………………………………………………10分
22.(1)证明: 四边形
四边形 为矩形,
为矩形,
 ,……………………………………2分
,……………………………………2分
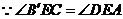 ,…………………………………………………………………3分
,…………………………………………………………………3分

 .………………………………………………………………4分
.………………………………………………………………4分
(2)∵△AED≌△CE ,
,
∴EA=EC,……………………………………………………………………………6分
∴点E在线段AC的垂直平分线上.…………………………………………………7分
(3)阴影部分的周长为AD+DE+EA+E +
+ C+EC,
C+EC,
=AD+DE+EC+EA+E +
+ C,
C,
=AD+DC+A +
+ C,
C,
=3+8+8+3=22.………………………………………………………………10分
21.解:(1)由题意可得m=2-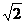 .…………………………………………………2分
.…………………………………………………2分
(2)把m的值代入得:|m-1|+(m+6)0
=|2-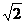 -1|+(2-
-1|+(2-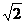 +6)0,……………………………………………………3分
+6)0,……………………………………………………3分
=|1-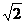 |+(8-
|+(8-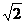 )0,…………………………………………………………5分
)0,…………………………………………………………5分
=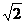 -1+1=
-1+1=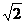 .…………………………………………………………………7分
.…………………………………………………………………7分
(3)P=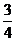 .………………………………………………………………………………9分
.………………………………………………………………………………9分
一、DBB CAD ABB CCC ABDC
17.- ; 18.1.2×104; 19.3; 20.9.
; 18.1.2×104; 19.3; 20.9.
26.(本小题满分1 3分)
3分)
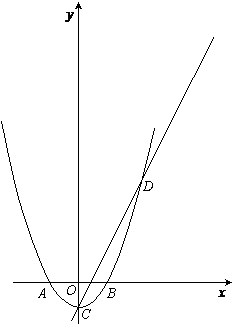 如图,在平面直角坐标系中,抛物线与x轴
如图,在平面直角坐标系中,抛物线与x轴
交于点A(-1,0)和点B(1,0),直线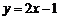
与y轴交于点C,与抛物线交于点C,D.
(1)求抛物线的解析式;
(2)求点A到直线CD的距离;
(3)平移抛物线,使抛物线的顶点P在直线
CD上,抛物线与直线CD的另一个交点为Q,点
G在y轴正半轴上,当以G,P,Q三点为顶点的
三角形为等腰直角三角形时,求出所有符合条件的
G点的坐标.
|
25.(本小题满分11分)




|
|
|
 .
.
探究展示:
(1)证明: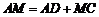 ;
;
|
|
|
 (2)
(2)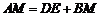 是否成立?
是否成立?

|
拓展延伸:
(3)若四边形ABCD是长与宽不相等的矩形,
其他条件不变,如图2,探究展示(1)、(2)中的结
论是否成立?请分别作出判断,不需要证明.
24.(本小题满分9分)
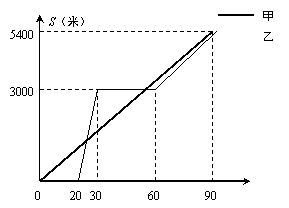 某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.
甲
某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.
甲 、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
 根据以上信息回答下列问题:
根据以上信息回答下列问题:
(1)乙出发后多长时间与甲相遇?
(2)要使甲到达景点C时,乙与
C的路程不超过400米,则乙从景点B[来源:Z。X。X。K]
步行到景点C的速度至少为多少?
(结果精确到0.1米/分钟)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com