23、（本小题满分12分）

　　 经统计分析，某市跨河大桥上的车流速度v（千米／小时）是车流密度x（辆／千米）

　 　的函数，当桥上的车流密度达到220辆／千米时，造成堵塞，此时车流速度为O千米/小时；当车流密度不超过20辆／千米时，车流速度为80千米／小时．研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．

　　 (1)求大桥上车流密度为100辆／千米时的车流速度．

　　 (2)在交通高峰时段，为使大桥上的车流速度大于40千米／小时且小于60千米／小时时，应控制大桥上的车流密度在什么范围内？

　 　(3)车流量（辆／小时）是单位时间内通过桥上某观测点的车辆数，即：车流量=车流速度×车流密度．求大桥上车流量y的最大值．

22．（本小题满分1 2分）

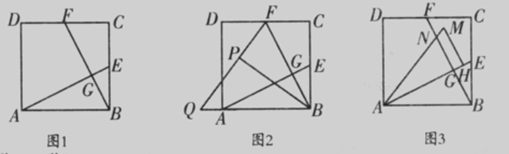
　　 如图1，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE、BF，交点为G．

　　 (1)求证：AE⊥BF；

　　 (2)将△BCF沿BF对折，得到△BPF（如图2），延长FP交BA的延长线于点Q，求sin∠BQP的值；

　　 (3)将△ABE绕点A逆时针方向旋转，使边AB正好落在AE上，得到△AHM（如图3），若AM和BF相交于点N，当正方形ABCD的面积为4时，求四边形GHMN的面积．

21．（本小题满分10分）

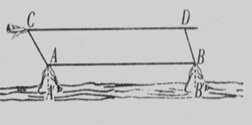如图，某海域有两个海拔均为200米的海岛A和海岛B，一勘测飞机在距离海平面垂直高度为1100米的空中飞行，飞行到点C处时测

得正前方一海岛顶端A的俯角是45⁰，然后：

　 　沿平行于AB的方向水平飞行1.99×10⁴米到

　 　达点D处，在D处测得正前方另一海岛顶端B

　 　的俯角是60⁰，求两海岛间的距离AB．

20．（本小题满分1 0分）

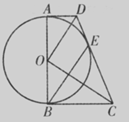　　 如图，在梯形ABCD中，AD∥BC，∠B=90⁰，以AB为直径作⊙O，恰与另一腰CD相切于点E，连接OD、OC、BE．

　　 (1)求证：OD∥BE；

(2)若梯形ABCD的面积是48，设OD=x，OC=y，且x+y=14，

求CD的长．

三、解答题

19．（本小题满分9分）

　　 今年我市把男生“引体向上”项目纳入学业水平体育考试内容．考试前某校为了解

　　 该项目的整体水平，从九年级220名男生中，随机抽取20名进行“引体向上”

　　 测试成绩（单位：个）如下：

　　 9　 12　 3　 13　 18 　8　 8　 4　 ■　 ，12

　　 13　 12　 9　 8　 12　 13　 18　 13　 12　 10

　　 其中有一数据被污损，统计员只记得11.3是这组样本数据的平均数．

　　 (1)求该组样本数据中被污损的数据和这组数据的极差；

　　 (2)请补充完整下面的频数、频率分布表和频数分布直方图；

(3)估计在学业水平体育考试中该校九年级有多少名男生能完成11个以上（包含11个）“引体向上”？

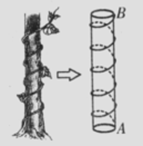
18。我国古代有这样一道数学问题：“枯木一根直立地上'高二丈

　　 周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几

何？，题意是：如图所示，把枯木看作一个圆柱体，因一丈是

十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A

处缠绕而上，绕五周后其末端恰好到达点B处．则问题中葛藤

的最短长度是　　 　　尺．

17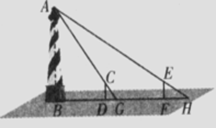．如图，某水平地面上建筑物的高度为AB，在点D和

点F处分别竖立高是2米的CD和EF，两标杆相隔

52米，并且建筑物AB、标杆CD和EF在同一竖直平

面内，从标杆CD后退2米到点G处，在G处测得建

筑物顶端A和标杆顶端C在同一条直线上；从标杆

FE后退4米到点H处，在H处测得建筑物顶端A和

标杆顶端E在同一条直线上，则建筑物的高是　　 米．

16．已知一组数据一3，x，一2, 3，1，6的中位数为1，则其方差为　　　　　　　 　.

15．如图，两个半径均为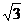的⊙O₁与⊙O₂相交于A、B两点,且

每个圆都经过另一个圆的圆心，则图中阴影部分的面积为

　　　 　　．（结果保留π）

14．计算：8²⁰¹⁴×(一0.125)²⁰¹⁵=　　　　　 　.