24（本题满分9分）

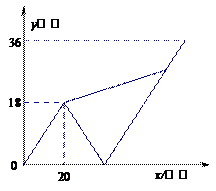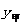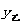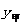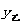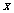甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发，骑电动车行驶20分钟时发现忘带相机，甲下车前往，乙骑电动车按原路返回.乙取相机后（在学校取相机所用时间忽略不计），骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲方与学校相距（千米），乙与学校相离（千米），甲离开学校的时间为t（分钟）. 、与之间的函数图象如图所示，结合图象解答下列问题：

（1）电动车的速度为　　　　 千米/分钟；

（2）甲步行所用的时间为　　　　　 分；

（3）求乙返回到学校时，甲与学校相距多远？

25(本题满分14分)

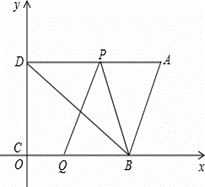直角梯形ABCD在直角坐标系中的位置如图所示，AD∥BC，∠DCB=90°，BC=16，DC=12，AD=21．动点P从点D出发，沿射线DA的方向以每秒2个单位长的速度运动，动点Q从点B出发，在线段BC上以每秒1个单位长的速度向点C运动，点P、Q分别从点D、B同时出发，当点Q运动到与点C重合时，点P随之停止运动．设运动时间为t（秒） 　（1）设△BPQ的面积为S，求S与t之间的函数关系式．

（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？ （3）是否存在某一时刻t，使直线PQ恰为过B、C两点的抛物线的对 称轴？若不存在，能否改变其中一个点的运动速度，使某一时刻直线PQ是过B、C两点的抛物线的对称轴，并求出改变后的速度．

（4）是否存在某一时刻t，使得PQ⊥BD？若存在，求出t的值；若　　 不存在，请说明理由．

23、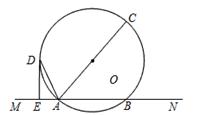（本小题满分9分）

　 已知，如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．

（1）求证：DE是⊙O的切线；

（2）若DE=6cm，AE=3cm，求⊙O的半径．

22、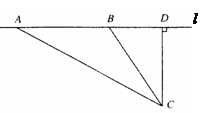（本小题满分6分）

　 校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载。某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，，再在笔直的车道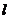上确定点D，使CD与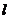垂直，测得CD的长等于21米，在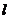上点D的同侧取点A，B，使∠CAD=30°，∠CBD=60°。

　 （1）求AB的长（精确到0.1米，参考数据：）；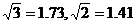

　 （2）已知本路段对校车限速为40千米/小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速？请说明理由。

21、（本小题满分8分）

在一个不透明的口袋里装有分别标注2，4，6的3个小球（小球除数字不同外，其余都相同），另有3张背面完全一样、正面分别写有数字6，7，8的卡片。现从口袋中任意摸出一个小球，再从这3张背面朝上的卡片中任意摸出一张卡片。

（1）请你用列表或画树状图的方法，表示出所有可能出现的结果；

（2）小红和小莉做游戏，制定了两个游戏规则：

规则1：若两次摸出的数字，至少有一次是“6”，小红赢；否则，小莉赢。

规则2：若摸出的卡片上的数字是球上数字的整数倍时，小红赢；否则，小莉赢。

小红要想在游戏中获胜，她会选择哪一种规则，并说明理由。

20、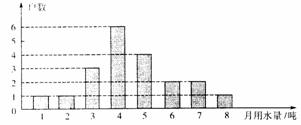（本小题满分7分）

为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图。

（1）小明一共调查了多少户家庭？

（2）求所调查家庭5月份用水量的众数、平均数；

（3）若该小区有400户居民，请你估计这个小区5月份的用水量。

19、（本小题满分6分）

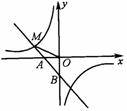如图所示，一次函数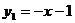的图象与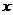轴交于点A，与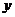轴交于点B，与反比例函数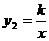图象的一个交点为M（）。

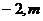（1）求反比例函数的解析式；

（2）求△MOB的面积。

18、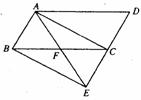（本小题满分6分）

如图，将□ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F。

（1）求证：△ABF≌△ECF；

（2）若∠AFC=2∠D，连接AC，BE，求证：四边形ABEC是矩形。

17、（本小题满分5分）

据林业专家分析，树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物，具有滞尘净化空气的作用。已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克，若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同，求一片国槐树叶一年的平均滞尘量。

三、解答题

16、（本小题满分5分）

　　 先化简，再求值：，其中．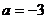

15、平面直角坐标系中，⊙M的圆心坐标为（0,2），半径为1，点N在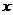轴的正半轴上，如果以点N为圆心，半径为4的⊙N与⊙M相切，则圆心N的坐标为　　　　　　　　 。