
21.(12分)设O为坐标原点,A(-,0),点M在定直线x=-p(p>0)上移动,点N在线段MO的延长线上,且满足=.
(Ⅰ)求动点N的轨迹方程,并说明轨迹是什么曲线?
(Ⅱ)若|AN|的最大值≤,求p的取值范围.
20.(12分)某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100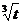 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
19.(12分)定义域均为R的奇函数f(x)与偶函数g(x)满足f(x)+g(x)=10x.
(Ⅰ)求函数f(x)与g(x)的解析式;
(Ⅱ)求函数f(x)的反函数;
(Ⅲ)证明:g(x1)+g(x2)≥
*(Ⅳ)试用f(x1),f(x2),g(x1),g(x2)表示f(x1-x2)与g(x1+x2).
(Ⅲ) 记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为 .当
.当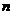 取多少时,
取多少时, 最大?
最大?
(Ⅱ)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅰ)试用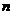 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率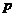 ;
;
18.(12分)一个口袋中装有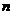 个红球(
个红球( 且
且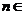 N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
N)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
17.(12分)已知△ABC中,A,B,C的对边分别为a,b,c,且()2=?+?+?.
(Ⅰ)判断△ABC的形状,并求sinA+sinB的取值范围;
*(Ⅱ)若不等式a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a,b,c都成立,求k的取值范围.
*16.函数f(x)=xn+(1-x)n,x∈(0,1),n∈N*.记y=f(x)的最小值为an,则a1+a2+…+a6=___.
*15.已知函数 ,若
,若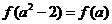 ,则实数a=
.
,则实数a=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com