1.从小到大，我们在文学作品的滋养中成长。假如要把你读过的文学作品安放到书架上，请为这个书架起一个别致而有意义的名字，将这个名字规范、工整地写在田字格里。(不超过6个字)(2分)

30、(本小题共10分)已知：AB切⊙O于点B，线段AB的垂直平分线CF交AB于点C，交⊙O于点D、E．设点M是射线CF上的任一点，CM=a，连接AM，若CB=3，DE=8．

(1)求⊙O 半径及线段CD的长；

(2)当M在线段DE(不含端点E)上时，延长AM交⊙O于点N，连接NE，若

△ACM∽△NEM，求NE；

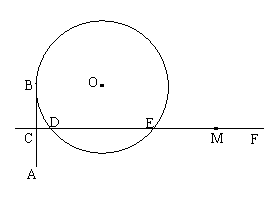
(3)当点M在射线EF上时，若a为小于17的正数，问是否存在这样的a，使得直线AM与⊙O相切？若存在，求出a的值；若不存在，试说明理由．

29、(本小题共10分)在一次科学探究实验中，小明将半径为6cm的圆形滤纸片按图1所示的步骤进行折叠，并围成圆锥形．

(1)求用半径为6cm的圆形滤纸按图示方法进行两次对折，滤纸片重叠部分为三层，且每层为圆时所做成的圆锥的锥角(锥角：即圆锥经过轴的截面上两条母线的夹角，例如图1中∠AOB)；

(2)取一漏斗，上部的圆锥形内壁(忽略漏斗管口处)的母线OE长为8cm，开口圆(即圆锥底面圆)的直径为8cm(如图2)．当(1)中的滤纸围成的圆锥形放入漏斗中时，能否紧贴此漏斗的内壁(忽略漏斗管口处)，请你通过比较两个圆锥锥角的大小来说明；

(3)假设有一特殊规格的漏斗(如图3)，其母线长为6cm，开口圆的直径为7.2cm，现将同样大小的滤纸围成重叠部分为三层的圆锥形，放入此漏斗中，且能紧贴漏斗内壁。问重叠部分每层的面积应为多少？(结果用π表示)

	图1

28、(本小题共8分)如图，已知⊙O₁与⊙O₂相交于A、B两点，且点O₂在⊙O₁上．

(1)如图①，AD是⊙O₂的直径，连接DB并延长交⊙O₁于点C，试说明CO₂⊥AD；

(2)如图②，如果AD是⊙O₂的一条弦，连接DB并延长交⊙O₁于点C，那么CO₂所在的直线是否仍与AD垂直？说明你的理由．

		图①

27、(本小题共8分)某商场进了一批服装，进货单价为50元，若按每件60元出售，则可销售800件；若每件每提价2元出售，则其销售量就减少40件，现预算要获利润12000元，应按每件多少元出售？这时应进多少件服装？

26、(本小题共12分)姚明是我国著名的篮球运动员，他在2005－2006赛季NBA常规赛中表现非常优异．下面是他在这个赛季中，分期与“超音速队”和“快船队”各四场比赛中的技术统计．

(1)请分别计算姚明在对阵“超音速”队的四场比赛中，四场得分的平均分是多少？在对阵“快船”队的四场比赛中，四场得分的平均分是多少?

(2)请你从得分的角度利用方差进行分析，姚明在与“超音速”和“快船”的比赛中，对阵哪一个队的发挥更稳定?

　(3)如果规定“综合得分”为：平均每场得分×l+平均每场篮板×1．5十平均每场失误×(－1.5)，且综合得分越高表现越好，那么请你利用这种评价方法，来比较姚明在分别与“超音速”和“快船”的各四场比赛中，对阵哪一个队表现更好?

25、(本小题共8分)如图所示，以Rt△ABC的直角边AB为直径的⊙O交斜边AC于点E，点D是BC边的中点，连接ED．

(1)试说明：ED是⊙O的切线；

(2)若⊙O 直径为6，线段BC长为8，求AE的长．

24、(本小题共7分)如图，阴影部分是由4段以正方形边长的一半为半径的圆弧围成的，这个图形被称作为斯坦因豪斯图形．

(1)请你在右边已作好的正方形中作出这四段弧，将其补成斯坦因豪斯图形(不要求写作法，留下作图痕迹，阴影部分用斜线填涂)．

(2)若图中正方形的边长为10，请你求出图中阴影部分的面积．

23、(本小题共7分)已知：如图，⊙O是△ABC的外接圆，圆心O在这个三角形的高CD上，E、F分别是边AC和BC的中点．判断四边形CEDF的形状并说明理由．

22、(本小题共7分)已知关于x的方程x²-2(m+1)x+m²=0。

(1)当m为何值时，方程有两个实数根？

(2)为m选取一个合适的整数，使方程有两个不相等的实数根，并求出这两个根．