25．(本小题满分12分)

有一根直尺的短边长2cm，长边长10cm，还有一块锐角为45°的直角三角形纸板，其中直角三角形纸板的斜边长为12cm．按图14-1的方式将直尺的短边DE放置在与直角三角形纸板的斜边AB上，且点D与点A重合．若直尺沿射线AB方向平行移动，如图14-2，设平移的长度为x(cm)，直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S cm ²)．

(1)当x=0时，S=_____________；当x = 10时，S =______________；

(2)当0＜x≤4时，如图14-2，求S与x的函数关系式；

(3)当6＜x＜10时，求S与x的函数关系式；

(4)请你作出推测：当x为何值时，阴影部分的面积最大？并写出最大值．

(说明：问题(4)是额外加分题，加分幅度为1-4分)

24．(本小题满分12分)

某商店经营一批进价为2元的小商品，在市场营销的过程中发现：如果该商品按最低价3元销售，日销售量为18件，如果单价每提高1元，日销售量就减少2件．设销售单价为x(元)，日销售量为y(件)．

(1)写出日销售量y(件)与销售单价x(元)之间的函数关系式；

(2)设日销售的毛利润(毛利润=销售总额-总进价)为P(元)，写出毛利润P(元)与销售单价x(元)之间的函数关系式；

(3)在图13所示的坐标系中画出P关于x的函数图象的草图，并标出顶点的坐标；

(4)观察图象，说出当销售单价为多少时，日销售的毛利润最高？是多少？

22．(本小题满分8分)

如图11-1，在△ABC中，∠C=90°，AC=4，BC=3，四边形DEFG为△ABC的内接正方形，若设正方形的边长为x，容易算出x的长为．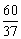

探究与计算：

(1)如图11-2，若三角形内有并排的两个全等的正方形，它们组成的矩形内接于

△ABC，则正方形的边长为　　　　　 ；

(2)如图11-3，若三角形内有并排的三个全等的正方形，它们组成的矩形内接于

△ABC，则正方形的边长为　　　　　 ．

猜想与证明：

如图11-4，若三角形内有并排的n个全等的正方形，它们组成的矩形内接于△ABC，请你猜想正方形的边长是多少？并对你的猜想进行证明．

21．(本小题满分8分)

某市自来水公司为鼓励居民节约用水，采取每月

用水量分段收费的办法，每户居民应交水费y(元)

与用水量x(吨)之间的函数关系如图10所示．

(1)分别求出当0≤x≤15和x≥15时，y与x的

函数关系式；

(2)若一用户在某月的用水量为21吨，则应交

水费多少元？

20．(本小题满分8分)

某少儿活动中心在“六·一”活动中，举行了一次转盘摇奖活动．

如图9是一个可以自由转动的转盘，当转动停止时，指针落在哪一个

区域就可以获得相应的奖品(落在分界线上时重新摇奖)．下表是活动

进行中统计的有关数据．

(1)计算并完成表格：

转动转盘的次数n 100 150 200 500 800 1000 落在“铅笔”区域中的次数m 68 111 136 352 556 701 落在“铅笔”区域中的频率

19．(本小题满分8分)

甲、乙两个商场在同一周内经营同一种商品，每天的获利情况如下表：

(1)请你计算出这两个商场在这周内每天获利的平均数，并说明这两个商场本周内总的获利情况；

(2)在图8所示的网格图内画出两个商场每天

获利的折线图；(甲商场用虚线，乙商场用

实线)

(3)根据折线图请你预测下周一哪个商场的获

利会多一些？并简单说出你的理由．

18．(本小题满分7分)

观察右表中数字的排列规律，回答下面

的问题

①表中第1行第5列的数字是　　　　 ；

②表中第5行第4列的数字是　　　　 ；

③请用关于n的代数式表示表中第3列

第n行的数为　　　　　　 ；

④数字2006的位置是第　　　 行，第　　　 列．

17．(本小题满分7分)

如图7，小丽在观察某建筑物．

(1)请你根据小亮在阳光下的投影，画出建筑物在阳光下的投影．

(2)已知小丽的身高为，在同一时刻测得小丽和建筑物的投影长分别为和，求建筑物的高．

16．(本小题满分7分)

已知：a=2，求(1+)·(a²－1)值．