28. 矩形ABCO的面积为10，OA比OC大3，E为BC的中点，以OE为直径的⊙O'交 轴于D，DF⊥AE于F。

(1) 求OA、OC的长。

(2) 求DF长；

(3) P为边BC上一动点,设△ABP的面积为，△OPC的面积为，求的函数关系式，并写出的取值范围。

　(4) 直线BC上是否存在点Q，使∠AQO = 90°，若存在，求出Q点坐标，若不存在，请说明理由。　　　　　　　　　　　　　　　　　　　 (12分)

27. 某校为选派一名学生参加全市实践活动技能竞赛，分别对A、B两位同学加工的直径为20mm的零件进行测试，测试结果如图(单位：mm)

根据测试得到的有关数据，解答下列问题：

	平均数	方差	完全符合要求的个数
A	20	0.026	2
B	20		5

(1) 考虑平均数与完全符合要求的个数，你认为谁的成绩好些；

(2) 计算的大小，考虑平均数与方差，说明谁的成绩好些；

(3) 由图中折线走势及竞赛中加工零件个数远远超过10个的实际情况下，你认为派谁去参加较合适？说明你的理由。　　　　　　　　　　　　 (10分)

26. 某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面。

　　 (1) 请你补全这个输水管道的圆形截面；

　　 (2) 若这个输水管道有水部分的水面宽AB = 16cm，水面最深地方的高度为4cm，求这个圆形截面的半径。　　　　　　　　　　　　　　　 (10分)

25. 如图，AB是⊙O的直径，PB与⊙O相切于点B，弦AC//OP。

(1) 求证：PC是⊙O的切线；

(2) 若BC = 8，AB = 10，求BP的长。　　　 (10分)

24. 如图，已知菱形ABCD，AE⊥BC于E，AF⊥CD于F。　

　　 (1) 求证：CE = CF；

　　 (2) 若菱形边长为8，E是BC的中点，求菱形的面积。　 (10分)

23．将进货单价为40元的商品按50元售出时，能卖出500个，已知这种商品每涨价0.1元时，其销量就减少1个，问：为了赚得9000元的利润，售价应定为多少？这时应进货多少个？　 (9分)

22. 先化简后求值：

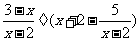　　 ，其中是方程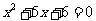的根。　 (8分)

21. 　　(8分)

20. △ABC内接于⊙O，D为的中点，BD交AC于点E，若DC = 4，DB = 8，则

DE=____________。

19. 如图，AB是⊙O的直径，弦AB、CD相交于E，∠ACD = 60⁰，∠ADC = 50⁰，则∠CEB = __________。

　　　　　　　　 第18题　　　　　　　　　 第19题　　　　　　　　 第20题