1．根据拼音写汉字，并给加点的字注音。(5分)

抽chù (　　 )　　 　　　　 相得益zhāng (　　 )　　 　　　 一拍即hé (　　 )

甜nì (　　 )　　 　　　　　 略胜一chóu (　　 )　　 　　　　　　　 迫不jí (　　 )待

畸形(　　 )　　 　　　　　　 逞能(　　 )　　 　　　　　　　　　 砭骨(　　 )　　 　　　　　　 污秽(　　 )

26．如图13－1，操作：把正方形CGEF的对角线

CE放在正方形ABCD的边BC的延长线上(CG＞BC)，

取线段AE的中点M。

探究：线段MD、MF的关系，并加以证明。

说明：(1)如果你经历反复探索，没有找到解决问题

的方法，请你把探索过程中的某种思路写出来(要求

至少写3步)；(2)在你经历说明(1)的过程之后，

可以从下列①、②、③中选取一个补充或更换已知条件，

完成你的证明。

注意：选取①完成证明得10分；选取②完成证明得

7分；选取③完成证明得5分。

①　　 DM的延长线交CE于点N，且AD＝NE；

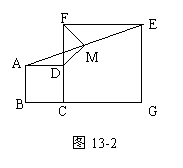
②　　 将正方形CGEF绕点C逆时针旋转45°(如图13－2)，

其他条件不变；③在②的条件下且CF＝2AD。

附加题：将正方形CGEF绕点C旋转任意角度后

(如图13－3)，其他条件不变。探究：线段MD、

MF的关系，并加以证明。

25．如图12，P是y轴上一动点，是否

存在平行于y轴的直线x＝t，使它与直线

y＝x和直线分别交于点D、E

(E在D的上方)，且△PDE为等腰直角三

角形。若存在，求t的值及点P的坐标；

若不存在，请说明原因。

24．已知A₁、A₂、A₃是抛物线上的三点，

A₁B₁、A₂B₂、A₃B₃分别垂直于x轴，垂足为B₁、B₂、

B₃，直线A₂B₂交线段A₁A₃于点C。

(1)　　　 如图11－1，若A₁、A₂、A₃三点的横坐标依次

为1、2、3，求线段CA₂的长。

(2)如图11－2，若将抛物线改为抛物线

，A₁、A₂、A₃三点的横坐标为连续

整数，其他条件不变，求线段CA₂的长。

(3)若将抛物线改为抛物线，

A₁、A₂、A₃三点的横坐标为连续整数，其他条件不变，

请猜想线段CA₂的长(用a、b、c表示，并直接写出答案)。

23．甲车在弯路作刹车试验，收集到的数据如下表所示：

速度x(千米/小时)	0	5	10	15	20	25	…
刹车距离y(米)	0		2		6		…

(1)　　　 请用上表中的各对数据(x，y)作为点的坐标，

速度x(千米/时)的函数图象，并求函数的解析式。

(2)在一个限速为40千米/时的弯路上，甲、乙两车相向

而行，同时刹车，但还是相撞了。事后测得甲、乙两车的

刹车距离分别为12米和10.5米，又知乙车的刹车距离y(米)与速度x(千米/时)满足函数，请你就两车的速度方面分析相撞的原因。

22．如图9－1、9－2、9－3、…、9－n，M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连结OM、ON。

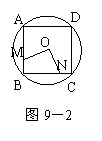
(1)求图9－1中∠MON的度数；

(2)图9－2中∠MON的度数是_________，图9－3中∠MON的度数是_________；

(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案)。

21．如图8，△ABC和△A’B’C’关于直线MN对称，

△A’B’C’和△A’’B’’C’’关于直线EF对称。

(1)　　　 画出直线EF；

(2)　　　 直线MN与EF相交于点O，试探究∠BOB’’

　 与直线MN、EF所夹锐角α的数量关系。

20．有一个抛两枚硬币的游戏，规则是：若出现两个正面，则甲赢；若出现一正一反，则乙赢；若出现两个反面，则甲、乙都不赢。

(1)　　　 这个游戏是否公平？请说明理由；

(2)　　　 如果你认为这个游戏不公平，那么请你改变游戏规则，设计一个公平的游戏；如果你认为这个游戏公平，那么请你改变游戏规则，设计一个不公平的游戏。

19．在数学活动中，小明为了求的值(结果用n表示)，设计如图7－1所示的几何图形。

(1)请你利用这个几何图形求

的值为__________。

(2)请你利用图7－2，再设计一个能求

的值的几何图形。

18．为了解某中学男生的身高情况，随机抽取若干名男生进行身高测量，将所得到的数据整理后，画出频数分布直方图(如图6)，图中从左到右依次为第1、2、3、4、5组。

(1)求抽取了多少名男生测量身高。

(2)身高在哪个范围内的男生人数最多？(答出是

　　 第几小组即可)

(3)若该中学有300名男生，请估计身高为170cm

及170cm以上的人数。