6、古诗词默写。(6分)

①受任于败军之际，　　　　　　　　　　　　　　 。(诸葛亮《出师表》)

　 ②　　　　　　　　　　　 ，西北望，射天狼。(苏轼《江城子·密州出猎》)

③白居易用“可怜身上衣正单，心忧炭贱愿天寒”表现卖炭翁的矛盾心理，在《观刈麦》中诗人也通过类似的句子“　　　　 　　　　　　　　，　　　　　　　　　　　　 。”来表达对劳动人民的同情。

④《沁园春·雪》中能够表明作者写作主旨和豪迈心情的句子是　　　　　　　　　

　　　　　　　　　　　　　　　　　　　 。

⑤写出你最喜欢的两个写景的句子：　　　　　　　　　　　　　　　　　　　　　　 。

　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　。

5、下列文学常识表述有误的一项(　　 )。(2分)

A、《诗经》是我国第一部诗歌总集，分为“风”“雅”“颂”三部分。

B、《我的叔叔于勒》选自短篇小说集《羊脂球》。

C、《陈涉世家》选自《史记》，作者是司马迁。

D、《故乡》和《藤野先生》都选自鲁迅的小说集《呐喊》。

4、仿写。　 (2分)

成熟的麦穗，低垂着头，那是在教我们谦虚，　　　　　　　　　　　　 ，　　　　

　　　　　　　　　　 ；温柔的水珠能滴穿岩石，那是在教我们坚韧。

3、下面语段中，划线的两处语病，请改正过来。(2分)

光阴是一把神奇而又无情的雕刻刀，在天地之间创造着种种奇迹。它能把坚冰融化成春风，把幼苗扶持成大树。当然，它也能把园林变成荒漠，①把废墟变成城市。你珍惜它，它就在你周围长出绿阴，结出沉甸甸的果实；你漠视它，它就化成轻烟；②消失得销声匿迹。

改正：①　　　　　　　　　　　　　　　　　　　　

　　　 ②　　　　　　　　　　　　　　　　　　　　

2、依次填入下面句子中横线上的词语恰当的一项是(　　 )。　 (2分)

2006年4月，胡锦涛主席访问美国，向全世界传达了这样一种信息：国际　　 、国内　　 、两岸　　　 是中国当前所需要努力的方向，中国将按照自己的步伐，发展目标与需要，来进行有计划的改革。

A、和平　 和谐　 和气　　　 B、和平　 和谐　 和解

C、和平　 和气　 和解　　　 D、和气　 和谐　 和解

1、根据拼音写汉字，给加点的字注音。(2分)

是鱼，就该畅(　　 )游于水中，是鸟，就该áo　　　 翔于蓝天；是云，就该降雪于大地；是马，就该chí　　　 骋于疆场；是人，就该挺直了背(　　 )梁。人生之追求，不也应该是这样的吗?

26．如图15，点P(－m，m²)抛物线：y = x²上一点，将抛物线E沿x轴正方向平移2m个单位得到抛物线F，抛物线F的顶点为B，抛物线F交抛物线E于点A，点C是x轴上点B左侧一动点，点D是射线AB上一点，且∠ACD = ∠POM．问△ACD能否为等腰三角形？

若能，求点C的坐标；若不能，请说明理由．

说明：⑴如果你反复探索，没有解决问题，请写出探索过程(要求至少写3步)；⑵在你完成⑴之后，可以从①、②中选取一个条件，完成解答(选取①得7分；选取②得10分)．

①m = 1；②m = 2．

附加题：如图16，若将26题“点C是x轴上点B左侧一动点”改为“点C是直线y =－m²上点N左侧一动点”，其他条件不变，探究26题中的问题．

25．如图14－1，P为Rt△ABC所在平面内任意一点(不在直线

AC上)，∠ACB = 90°，M为AB边中点．

操作：以PA、PC为邻边作平行四边形PADC，连续PM并

延长到点E，使ME = PM，连结DE．

探究：⑴请猜想与线段DE有关的三个结论；

⑵请你利用图14－2，图14－3选择不同位置的点P按上述方法操作；

⑶经历⑵之后，如果你认为你写的结论是正确的，请加以证明；

如果你认为你写的结论是错误的，请用图14－2或图14－3加以说明；

(注意：错误的结论，只要你用反例给予说明也得分)

⑷若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图14－4操作，并写出与线

段DE有关的结论(直接写答案)．

24．小明为了通过描点法作出函数的图象，先取自变量x的7个值满足：

x₂－x₁ = x₃－x₂ = … = x₇－x₆ = d，再分别算出对应的y值，列出表1：

　 表1：

记m₁ = y₂－y₁，m₂ = y₃－y₂，m₃ = y₄－y₃，m₄ = y₅－y₄，…；s₁ = m₂－m₁，s₂ = m₃－m₂，

s₃ = m₄－m₃，…

⑴判断s₁、s₂、s₃之间关系，并说明理由；

⑵若将函数“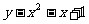”改为“”，列出表2：

表2：

其他条件不变，判断s₁、s₂、s₃之间关系，并说明理由；

⑶小明为了通过描点法作出函数的图象，列出表3：

表3：

由于小明的粗心，表3中有一个y值算错了，请指出算错的y值(直接写答案)．

23．如图13－1、图13－2分别是两个相同正方形、正六边形，其中一个正多边形的顶点在另一个正多边形外接圆圆心O处．

⑴求图13－1中，重叠部分面积与阴影部分面积之比；

⑵求图13－2中，重叠部分面积与阴影部分面积之比(直接出答案)；

⑶根据前面探索和图13－3，你能否将本题推广到一般的正n边形情况，(n为大于2的偶数)？若能，写出推广问题和结论；若不能，请说明理由．